题目内容
在半径为
的圆内，作内接等腰三角形，当底边上高为多少时，它的面积最大？
当
时，等腰三角形的面积最大．
解析:
如图，设圆内接等腰三角形的底边长为
，高为
，那么
，
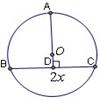
解得
，于是内接三角形的面积为：
，
从而
，
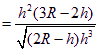令
，解得，由于不考虑不存在的情况，所在区间
上列表示如下：
|
|
|
|
|
|
|
|
|
|
|
| 增函数 | 最大值 | 减函数 |
由此表可知，当时，等腰三角形的面积最大．
练习册系列答案
相关题目
如图，在半径为r的圆内作内接正六边形，再作正六边形的内切圆，又在此内切圆内作内接正六边形，如此无限继续下去，设Sn为前n个圆的面积之和，则| lim |
| n→∞ |
| A、2πr2 | ||
B、
| ||
| C、4πr2 | ||
| D、6πr2 |
在半径为R的圆内作内接正方形，在这个正方形内作内切圆，又在圆内作内接正方形，如此无限次地作下去，试分别求所有圆的面积总和与所有正方形的面积总和．
如图，在半径为r的圆内作内接正六边形，再作正六边形的内切圆，又在此内切圆内作内接正六边形，如此无限继续下去，设Sn为前n个正六边形的面积之和，则