题目内容
3.己知角φ的终边经过点P(5,-12),函数f(x)=sin(ωx+φ)(ω>0),满足对任意的x,存在x1,x2使得f(x1)≤f(x)≤f(x2)成立,且|x1-x2|的最小值为$\frac{π}{4}$,则f($\frac{π}{4}$)的值为( )| A. | $\frac{5}{13}$ | B. | -$\frac{5}{13}$ | C. | $\frac{12}{13}$ | D. | -$\frac{12}{13}$ |
分析 利用任意角的三角函数的定义求得sinφ的值,利用正弦函数的图象的特征求得ω,再利用诱导公式求得f($\frac{π}{4}$)的值.
解答 解:∵角φ的终边经过点P(5,-12),由三角函数定义知:$sinφ=-\frac{12}{13}$,
由已知存在x1,x2使得f(x1)≤f(x)≤f(x2)成立,且|x1-x2|的最小值为$\frac{π}{4}$,有 $T=\frac{π}{2}$=$\frac{2π}{ω}$,
∴ω=4,∴f(x)=sin(4x+φ),故f($\frac{π}{4}$)=sin(π+φ)=-sinφ=$\frac{12}{13}$,
故选:C.
点评 本题主要考查任意角的三角函数的定义,诱导公式,正弦函数的图象的特征,属于基础题.

练习册系列答案
相关题目
14.已知i为虚数单位,则复数$\frac{3-4i}{1+i}$的虚部为( )
| A. | $-\frac{7}{2}$ | B. | $\frac{7}{2}$ | C. | $-\frac{7}{2}i$ | D. | $\frac{7}{2}i$ |
11.口袋中有编号分别为1、2、3的三个大小和形状相同的小球,从中任取2个,则取出的球的最大编号X的均值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | 2 | D. | $\frac{8}{3}$ |
8.在程序框图中,输入N=8,按程序运行后输出的结果是( )


| A. | 6 | B. | 7 | C. | 10 | D. | 12 |
15.已知复数z=$\frac{2}{i}$-i(其中i为虚数单位),则|z|=( )
| A. | 3 | B. | $\sqrt{5}$ | C. | 2 | D. | 1 |
12.下列程序输出的结果是( )
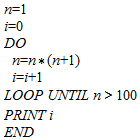
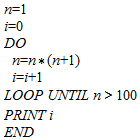
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
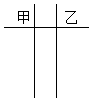 某赛季甲、乙两名篮球运动员每场比赛得分的原始记录如下:
某赛季甲、乙两名篮球运动员每场比赛得分的原始记录如下: