题目内容
3．
如图，四边形ABCD是正方形，SA=SB=SC=SD，P是棱SC上的点，M，N分别是棱SB，SD上的点，SP：PC=1：2，SN：ND=2：1，SM：MB=2：1求证：SA∥平面PMN．
分析 连结AC、BD，交于点G，取SC的中点H，连接BH、DH、GH，由已知条件推导出面HBD‖面PMN，再由中位线定理得到SA‖GH，由此能证明SA‖面PMN．
解答 
证明：连结AC、BD，交于点G，取SC的中点H，连接BH、DH、GH，
∵SP：PC=1：2，H是SC中点，
∴$\frac{SP}{PH}=\frac{SM}{MB}=\frac{SN}{ND}=2$，
∴PM∥HB，PN∥HD，
∵PM∩PN=P，HB∩HD=H，
PM?平面PMN，PN?平面PMN，HB?平面HBD，HD?平面HBD，
∴平面HBD‖平面PMN
∵四边形ABCD是正方形∴G是AC的中点，∴SA‖GH，
∵SA?平面BDH，GH?平面BDH，
∴SA∥平面BDH，又∵SA?平面PMN，
∴SA‖面PMN．
点评 本题考查线面平行的证明，将平面进行平行转化是解题关键，
练习册系列答案
七彩题卡口算应用一点通系列答案
相关题目
13．设$a={π^{0.3}}，b={log_π}3，c={log_3}sin\frac{2π}{3}$，则（ ）
| A． | a＞b＞c | B． | c＞a＞b | C． | b＞a＞c | D． | b＞c＞a |
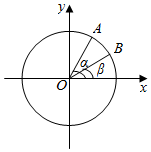如图，在平面直角坐标系中xOy中，以Ox轴的非负半轴为始边做两个锐角α，β，它们的终边分别与单位圆相交于A、B两点，已知A，B的横坐标分别为$\frac{\sqrt{2}}{10}$，$\frac{2\sqrt{5}}{5}$．
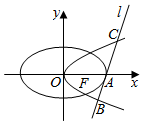如图，抛物线C：y2=8x的焦点为F，椭圆C2：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的右顶点为A，离心率为$\frac{1}{2}$，且F为线段OA的中点，O为坐标原点．