题目内容
17.已知角θ的终边在第三象限,tan2θ=-2$\sqrt{2}$,则sin2θ+sin(3π-θ)cos(2π+θ)-$\sqrt{2}$cos2θ=$\frac{2}{3}$.分析 由条件利用二倍角的正切公式求得tanθ的值,再利用诱导公式、同角三角函数的基本关系求得要求式子的值.
解答 解:角θ的终边在第三象限,tan2θ=-2$\sqrt{2}$=$\frac{2tanθ}{1{-tan}^{2}θ}$,∴tanθ=$\sqrt{2}$,或 tanθ=-$\frac{\sqrt{2}}{2}$(舍去)
则sin2θ+sin(3π-θ)cos(2π+θ)-$\sqrt{2}$cos2θ=sin2θ+sinθcosθ-$\sqrt{2}$cos2θ
=$\frac{{sin}^{2}θ+sinθcosθ-\sqrt{2}{•cos}^{2}θ}{{sin}^{2}θ{+cos}^{2}θ}$=$\frac{{tan}^{2}θ+tanθ-\sqrt{2}}{{tan}^{2}θ+1}$=$\frac{2}{3}$,
故答案为:$\frac{2}{3}$.
点评 本题主要考查二倍角的正切公式,诱导公式、同角三角函数的基本关系,属于基础题.

练习册系列答案
相关题目
7.一艘轮船从O点正东100海里处的A点处出发,沿直线向O点正北100海里处的B点处航行.若距离O点不超过r海里的区域内都会受到台风的影响,设r是区间[50,100]内的一个随机数,则该轮船在航行途中会遭受台风影响的概率约为( )
| A. | 20.7% | B. | 29.3% | C. | 58.6% | D. | 41.4% |
2.一个公司的一款新产品有若干销售店,为了解该产品的广告投入费用与销售额间的关系,该公司抽取了其中的五个销售店作为样本,统计出它们的广告投入费用x与销售额y,如下表:
(1)求销售额y对广告费用x的线性回归方程$\widehaty=\widehatbx+\widehata$;
(2)设k=$\frac{销售额}{广告费}$,若k≥10,则称该店为“盈利店”,把上述样品中“盈利店”的频率视作一个店是“盈利店”的概率,现另外再调查3个销售店,记这三个店中“盈利店”的个数为X,求X的分布列和数学期望.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:$\widehat{b}=\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}=\overline{y}-\widehat{b}\overline{x}$.
| x(万元) | 2 | 4 | 5 | 6 | 8 |
| y(万元) | 30 | 40 | 60 | 50 | 70 |
(2)设k=$\frac{销售额}{广告费}$,若k≥10,则称该店为“盈利店”,把上述样品中“盈利店”的频率视作一个店是“盈利店”的概率,现另外再调查3个销售店,记这三个店中“盈利店”的个数为X,求X的分布列和数学期望.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:$\widehat{b}=\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}=\overline{y}-\widehat{b}\overline{x}$.
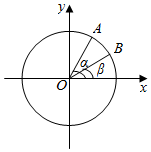 如图,在平面直角坐标系中xOy中,以Ox轴的非负半轴为始边做两个锐角α,β,它们的终边分别与单位圆相交于A、B两点,已知A,B的横坐标分别为$\frac{\sqrt{2}}{10}$,$\frac{2\sqrt{5}}{5}$.
如图,在平面直角坐标系中xOy中,以Ox轴的非负半轴为始边做两个锐角α,β,它们的终边分别与单位圆相交于A、B两点,已知A,B的横坐标分别为$\frac{\sqrt{2}}{10}$,$\frac{2\sqrt{5}}{5}$.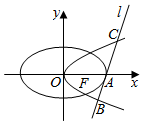 如图,抛物线C:y2=8x的焦点为F,椭圆C2:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右顶点为A,离心率为$\frac{1}{2}$,且F为线段OA的中点,O为坐标原点.
如图,抛物线C:y2=8x的焦点为F,椭圆C2:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右顶点为A,离心率为$\frac{1}{2}$,且F为线段OA的中点,O为坐标原点.