Question

4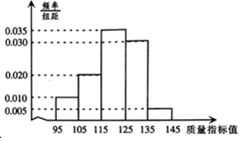．从某企业生产的某种产品中抽取500件，测量这些产品的一项质量指标值，由测量结果得如下频率分布直方图，则这500件产品质量指标值的样本方差s²是110（同一组中的数据用该组区间的中点值作代表）

Answer 1

分析 由频率分布直方图可估计样本特征数均值、方差．均值为每个矩形中点横坐标与该矩形面积积的累加值．方差是矩形横坐标与均值差的平方的加权平均值．

解答 解：由频率分布直方图得抽取产品的质量指标值的样本平均值为：
$\overline{x}$=100×0.010×10+110×0.020×10+120×0.035×10+130×0.030×10+140×0.005×10=120，
∴样本方差S²=（-20）²×0.1+（-10）²×0.2+0²×0.35+10²×0.3+20²×0.05=110．
∴这500件产品质量指标值的样本方差S²是110．
故答案为：110．

点评 本题考查频率分布直方图的应用，考查样本方差的求法，考查推理论证能力、运算求解能力，考查数形结合思想、转化化归思想，是基础题．