题目内容
13.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,且过点(-1,$\frac{3}{2}$),椭圆C的右焦点为A,点B的坐标为($\frac{1}{2}$,0).(Ⅰ)求椭圆C的方程;
(Ⅱ)已知纵坐标不同的两点P,Q为椭圆C上的两个点,且B、P、Q三点共线,线段PQ的中点为R,求直线AR的斜率的取值范围.
分析 (Ⅰ)由椭圆的离心率为$\frac{1}{2}$,且过点(-1,$\frac{3}{2}$),列出方程组,求出a,b,由此能求出椭圆C的方程.
(Ⅱ)依题意直线PQ过点($\frac{1}{2}$,0),且斜率不为0,设其方程为x=my+$\frac{1}{2}$,联立$\left\{\begin{array}{l}{x=my+\frac{1}{2}}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,得4(3m2+4)y2+12my-45=0,由此利用韦达定理、中点坐标公式,结合已知条件能求出直线AR的斜率的取值范围.
解答 解:(Ⅰ)∵椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,且过点(-1,$\frac{3}{2}$),
∴$\left\{\begin{array}{l}{e=\frac{c}{a}=\frac{1}{2}}\\{\frac{1}{{a}^{2}}+\frac{9}{4{b}^{2}}=1}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,解得a=2,b=$\sqrt{3}$,
∴椭圆C的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$.
(Ⅱ)依题意直线PQ过点($\frac{1}{2}$,0),且斜率不为0,
故可设其方程为x=my+$\frac{1}{2}$,
联立$\left\{\begin{array}{l}{x=my+\frac{1}{2}}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,消去x,得4(3m2+4)y2+12my-45=0,
设点P(x1,y1),Q(x2,y2),R(x0,y0),直线AR的斜率为k,
故${y}_{1}+{y}_{2}=-\frac{3m}{3{m}^{2}+4}$,${y}_{0}=-\frac{3m}{2(3{m}^{2}+4)}$,
∴${x}_{0}=m{y}_{0}+\frac{1}{2}=\frac{2}{3{m}^{2}+4}$,∴k=$\frac{{y}_{0}}{{x}_{0}-2}=\frac{m}{4{m}^{2}+4}$,
当m=0时,k=0,
当m≠0时,k=$\frac{1}{4m+\frac{4}{m}}$,故|4m+$\frac{4}{m}$|=4|m|+$\frac{4}{|m|}$,
∴0<$\frac{1}{4|m|+\frac{4}{|m|}}$≤$\frac{1}{8}$,
∴0<|k|$≤\frac{1}{8}$,∴-$\frac{1}{8}$$≤k≤\frac{1}{8}$,且k≠0,
综上所述,直线AR的斜率的取值范围是[-$\frac{1}{8},\frac{1}{8}$].
点评 本题考查椭圆方程的求法,考查直线斜率的取值范围的求法,考查推理论证能力、运算求解能力,考查转化化归思想,是中档题.

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案| A. | 4$\sqrt{3}$π | B. | $\frac{27\sqrt{3}π}{2}$ | C. | 27π | D. | 9π |
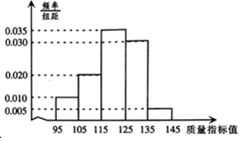 从某企业生产的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图,则这500件产品质量指标值的样本方差s2是110(同一组中的数据用该组区间的中点值作代表)
从某企业生产的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图,则这500件产品质量指标值的样本方差s2是110(同一组中的数据用该组区间的中点值作代表)