题目内容
8.已知二阶矩阵A=$[\begin{array}{l}{3}&{5}\\{0}&{-2}\end{array}]$和向量$\overrightarrow{β}$=$[\begin{array}{l}{1}\\{-1}\end{array}]$,则A6$\overrightarrow{β}$=$[\begin{array}{l}{64}\\{-64}\end{array}]$.(用数字表示)分析 求出矩阵A属于特征值-2的特征向量为$\overrightarrow{β}$=$[\begin{array}{l}{1}\\{-1}\end{array}]$,利用特征向量的定义与性质即可算出A6$\overrightarrow{β}$的值.
解答 解:矩阵A的特征多项式为f(λ)=(λ-3)(λ+2)
令f(λ)=0,得λ=3或λ=-2
将λ=-2代入二元一次方程组,得$\left\{\begin{array}{l}{-5x-5y=0}\\{0•x+0•y=0}\end{array}\right.$,取x=1得y=-1
∴矩阵A属于特征值-2的特征向量为$\overrightarrow{β}$=$[\begin{array}{l}{1}\\{-1}\end{array}]$,
∴A6$\overrightarrow{β}$=λ6$\overrightarrow{β}$=64$[\begin{array}{l}{1}\\{-1}\end{array}]$=$[\begin{array}{l}{64}\\{-64}\end{array}]$,
故答案为$[\begin{array}{l}{64}\\{-64}\end{array}]$.
点评 本题给出二阶矩阵,求矩阵A的特征值和特征向量.着重考查了特征向量的定义、求法及其性质等知识,属于中档题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
3.已知Sn是等差数列{an}的前n项和,若a1=-2017,$\frac{{{S_{2014}}}}{2014}-\frac{{{S_{2008}}}}{2008}$=6,则S2017=-2017.
20.函数$y=\frac{{{x^2}+7x+10}}{x+1}({x>-1})$的最小值为( )
| A. | 2 | B. | 7 | C. | 9 | D. | 10 |
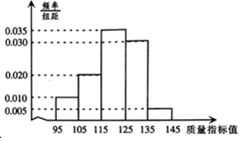 从某企业生产的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图,则这500件产品质量指标值的样本方差s2是110(同一组中的数据用该组区间的中点值作代表)
从某企业生产的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图,则这500件产品质量指标值的样本方差s2是110(同一组中的数据用该组区间的中点值作代表)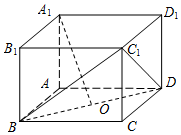 如图,长方体ABCD-A1B1C1D1中,AB=AD=2,AA1=$\sqrt{2}$,O为底面中心.
如图,长方体ABCD-A1B1C1D1中,AB=AD=2,AA1=$\sqrt{2}$,O为底面中心.