题目内容
9.已知(2x-1)(ax+2)5展开式中,不含x4项,且a≠0,则a=8.分析 先求出(ax+2)5展开式中含x3项与含x4项的系数,再求(2x-1)(ax+2)5展开式中x4项的系数,令其等于0,即可求出a的值.
解答 解:(ax+2)5展开式中,通项公式为Tr+1=${C}_{5}^{r}$•(ax)5-r•2r;
令5-r=3,解得r=2,
∴T3=4${C}_{5}^{2}$•a3•x3;
令5-r=4,解得r=1,
∴T2=2${C}_{5}^{1}$•a4•x4;
∴(2x-1)(ax+2)5展开式中,x4项的系数为:
2×4${C}_{5}^{2}$•a3-1×2${C}_{5}^{1}$•a4=0,
又a≠0,解得a=8.
故答案为:8.
点评 本题考查了利用二项式展开式的通项公式求特定项的系数问题,是基础题目.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
17.设直角坐标平面内与两个定点A(-2,0),B(2,0)的距离之差的绝对值等于2的点的轨迹是E,C是轨迹E上一点,直线BC垂直于x轴,则$\overrightarrow{AC}$$•\overrightarrow{BC}$=( )
| A. | -9 | B. | -3 | C. | 3 | D. | 9 |
14.已知复数z=$\frac{\sqrt{3}+i}{(1+i)^{2}}$,其中i为虚数单位,则|z|=( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
1.若复数z=(3+bi)(1+i)-2是纯虚数(b∈R),则|z|=( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
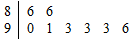 如图是某班8位学生诗词比赛得分的茎叶图,那么这8位学生得分的众数和中位数分别为93、92.
如图是某班8位学生诗词比赛得分的茎叶图,那么这8位学生得分的众数和中位数分别为93、92.