Question

已知三棱锥O-ABC，OA=5，OB=4，OC=3，∠AOB=∠BOC=60°，∠COA=90°，M、N分别是棱OA、BC的中点，则MN=

42

2

．

Answer 1

分析：取AB中点E，连结EN，ME，MC，计算MB，MC，BC，利用“平行四边形中对角线的平方和等于四条边的平方和”，可得结论．

解答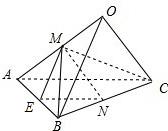：解：OA=5，OC=3，∠COA=90°，由勾股定理，AC=

34

，
取AB中点E，连结EN，ME，MC，
则ME和EN分别是三角形AOB和三角形ABC中位线，ME=2，EN=

34

2

，
在三角形OBM中，根据余弦定理，MB=

16+ 25 4 -2• 5 2 •4• 1 2

=

7

2

，
在三角形OMC中，根据勾股定理，MC=

25 4 +9

=

61

2

，
在三角形OBC中，根据余弦定理，BC=

9+16-2•3•4• 1 2

=

13

，
在三角形MBC中，根据“平行四边形中对角线的平方和等于四条边的平方和”，可得4MN2+13=2(

49

4

+

61

4

)
∴MN=

42

2

．

点评：本题考查三棱锥，考查余弦定理的运用，考查学生分析解决问题的能力，属于中档题．