题目内容
已知抛物线的顶点是椭圆C:
+
=1的中心O,焦点与该椭圆的右焦点重合.
(Ⅰ)求抛物线的方程;
(Ⅱ)设椭圆C的右准线交x轴于点Q,过点Q的直线l交抛物线于D、E两点.求△ODE面积的最小值;
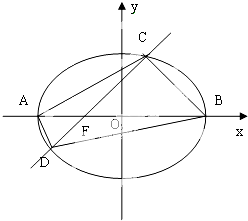
(Ⅲ)设A、B分别为椭圆C的左、右顶点,P为右准线上不同于点Q的任意一点,若直线AP、BP分别与椭圆相交于异于A、B的点M、N.求证:点B在以MN为直径的圆内.
| x2 |
| 4 |
| y2 |
| 3 |
(Ⅰ)求抛物线的方程;
(Ⅱ)设椭圆C的右准线交x轴于点Q,过点Q的直线l交抛物线于D、E两点.求△ODE面积的最小值;
(Ⅲ)设A、B分别为椭圆C的左、右顶点,P为右准线上不同于点Q的任意一点,若直线AP、BP分别与椭圆相交于异于A、B的点M、N.求证:点B在以MN为直径的圆内.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)设抛物线方程为y2=2px,(p>0).由a2-b2=4-3=1,得抛物线的焦点为(1,0),由此能示出抛物线的方程.
(Ⅱ)设直线l的方程为x=ay+4,D(x1,y1),E(x2,y2).联立
,整理得:y2-4ay-16=0,由此利用椭圆弦长公式能求出△ODE面积的最小值.
(Ⅲ) A(-2,0),B(2,0).设M(x0,y0)(-2<x0<2).由已知条件得
•
=
(x02-4+3y02).由此能证明点B在以MN为直径的圆内.
(Ⅱ)设直线l的方程为x=ay+4,D(x1,y1),E(x2,y2).联立
|
(Ⅲ) A(-2,0),B(2,0).设M(x0,y0)(-2<x0<2).由已知条件得
| BM |
| BP |
| 2 |
| x0+2 |
解答:
(Ⅰ)解:由题意,可设抛物线方程为y2=2px,(p>0).
由a2-b2=4-3=1,得c=1.
∴抛物线的焦点为(1,0),解得p=2.
∴抛物线的方程为y2=4x.
(Ⅱ)解:∵椭圆的右准线方程为x=4,∴Q(4,0),
设直线l的方程为x=ay+4,D(x1,y1),E(x2,y2).
联立
,整理得:y2-4ay-16=0,∴y1+y2=4a,y1y2=-16,
∴S△ODE=
|OQ|•|y1-y2|=2
=8
,
∴当a=0时,(S△ODE)min=16.
(Ⅲ)证明:∵A(-2,0),B(2,0).设M(x0,y0)(-2<x0<2).
∵M点在椭圆上,∴y0=
(4-x02).①
又直线AP的方程为y=
(x+2),则 P(4,
).
从而
=(x0-2,y0),
=(2,
).
∴
•
=2x0-4+
=
(x02-4+3y02).②
将①代入②,化简得
•
=
(2-x0).
∵2-x0>0,∴
•
>0,则∠MBP为锐角,从而∠MBN为钝角,
故点B在以MN为直径的圆内.
由a2-b2=4-3=1,得c=1.
∴抛物线的焦点为(1,0),解得p=2.
∴抛物线的方程为y2=4x.
(Ⅱ)解:∵椭圆的右准线方程为x=4,∴Q(4,0),
设直线l的方程为x=ay+4,D(x1,y1),E(x2,y2).
联立
|
∴S△ODE=
| 1 |
| 2 |
| (y1+y2)2-4y1y2 |
| a2+4 |
∴当a=0时,(S△ODE)min=16.
(Ⅲ)证明:∵A(-2,0),B(2,0).设M(x0,y0)(-2<x0<2).
∵M点在椭圆上,∴y0=
| 3 |
| 4 |
又直线AP的方程为y=
| y0 |
| x0+2 |
| 6y0 |
| x0+2 |
从而
| BM |
| BP |
| 6y0 |
| x0+2 |
∴
| BM |
| BP |
| 6y02 |
| x0+2 |
| 2 |
| x0+2 |
将①代入②,化简得
| BM |
| BP |
| 5 |
| 2 |
∵2-x0>0,∴
| BM |
| BP |
故点B在以MN为直径的圆内.
点评:本题考查抛物线方程的求法,考查三角形面积的最小值的求法,考查点在圆内的证明,解题时要认真审题,注意椭圆弦长公式的合理运用.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
如图,P是△ABC所在的平面内一点,且满足
+
=
,D,E是BP的三等分点,则( )

| BA |
| BC |
| 2 |
| 3 |
| BP |

A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
 已知椭圆M:
已知椭圆M: 已知椭圆C:
已知椭圆C: 如图,已知角α的终边在第二象限,且与单位圆交于点P(m,
如图,已知角α的终边在第二象限,且与单位圆交于点P(m,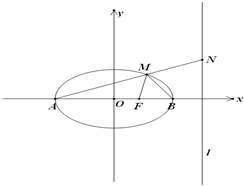 一束光线从点F1(-1,0)出发,经直线l:x+2y+6=0上一点M反射后,恰好穿过点F2(1,0).
一束光线从点F1(-1,0)出发,经直线l:x+2y+6=0上一点M反射后,恰好穿过点F2(1,0).