题目内容
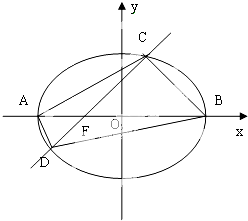 已知椭圆M:
已知椭圆M:| x2 |
| a2 |
| y2 |
| 3 |
(Ⅰ)求椭圆方程;
(Ⅱ)若直线l的斜率为
| 1 |
| 2 |
3
| ||
| 5 |
(Ⅲ)记△ABD与△ABC的面积分别为S1和S2,求|S1-S2|的最大值.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)由焦点F坐标可求c值,根据a,b,c的平方关系可求得a值;
(Ⅱ)写出直线方程,可得切线方程,再利用两条直线间的距离公式,即可得出结论;
(Ⅲ)当直线l不存在斜率时可得,|S1-S2|=0;当直线l斜率存在(显然k≠0)时,设直线方程为y=k(x+1)(k≠0),与椭圆方程联立消y可得x的方程,根据韦达定理可用k表示x1+x2,x1x2,|S1-S2|可转化为关于x1,x2的式子,进而变为关于k的表达式,再用基本不等式即可求得其最大值
(Ⅱ)写出直线方程,可得切线方程,再利用两条直线间的距离公式,即可得出结论;
(Ⅲ)当直线l不存在斜率时可得,|S1-S2|=0;当直线l斜率存在(显然k≠0)时,设直线方程为y=k(x+1)(k≠0),与椭圆方程联立消y可得x的方程,根据韦达定理可用k表示x1+x2,x1x2,|S1-S2|可转化为关于x1,x2的式子,进而变为关于k的表达式,再用基本不等式即可求得其最大值
解答:
解:(Ⅰ)因为椭圆的焦点为F(-1,0),所以c=1,
又b2=3所以a2=4,
所以椭圆方程为
+
=1…(2分)
(Ⅱ)直线l的斜率为
,方程为x-2y+1=0,设切线y=
x+b,
与椭圆方程联立,得4x2+4bx+4b2-12=0,
由△=0得b=±2,
∴切线方程为x-2y±4=0,
x-2y+4=0与l的距离为
=
,x-2y-4=0与l的距离为
=
>
∴椭圆上到l的距离为
的点的个数为3个;
(Ⅲ)当直线l无斜率时,直线为x=-1,此时C(-1,-
),D(-1,
)
△ABD与△ABC面积相等,|S1-S2|=0 …(7分)
当直线l斜率存在时,显然k≠0,
设直线为y=k(x+1)(k≠0)联立椭圆方程得(3+4k2)x2+8k2x+4k2-12=0
显然△>0,且x1+x2=-
,x1•x2=
…(8分)
此时|S1-S2|=
•|AB|•||y1|-|y2||=2|y1+y2|=2|k(x1+1)+k(x2+1)|=2|k(x1+x2)+2k|=
…(10分)
因为k≠0,上式=
≤
=
当k=±
时等号成立
综上的,|S1-S2|的最大值为
…(12分)
又b2=3所以a2=4,
所以椭圆方程为
| x2 |
| 4 |
| y2 |
| 3 |
(Ⅱ)直线l的斜率为
| 1 |
| 2 |
| 1 |
| 2 |
与椭圆方程联立,得4x2+4bx+4b2-12=0,
由△=0得b=±2,
∴切线方程为x-2y±4=0,
x-2y+4=0与l的距离为
| |4-1| | ||
|
3
| ||
| 5 |
| |-4-1| | ||
|
| 5 |
3
| ||
| 5 |
∴椭圆上到l的距离为
3
| ||
| 5 |
(Ⅲ)当直线l无斜率时,直线为x=-1,此时C(-1,-
| 3 |
| 2 |
| 3 |
| 2 |
△ABD与△ABC面积相等,|S1-S2|=0 …(7分)
当直线l斜率存在时,显然k≠0,
设直线为y=k(x+1)(k≠0)联立椭圆方程得(3+4k2)x2+8k2x+4k2-12=0
显然△>0,且x1+x2=-
| 8k2 |
| 3+4k2 |
| 4k2-12 |
| 3+4k2 |
此时|S1-S2|=
| 1 |
| 2 |
| 12|k| |
| 3+4k2 |
因为k≠0,上式=
| 12 | ||
|
| 12 | ||||
2
|
| 3 |
| ||
| 2 |
综上的,|S1-S2|的最大值为
| 3 |
点评:本题考查直线与圆锥曲线的位置关系及椭圆的标准方程的求解,考查学生综合运用知识分析问题解决问题的能力,难度较大.

练习册系列答案
相关题目
一所中学有高一、高二、高三共三个年级的学生900名,其中高一学生400名,高二学生300名,高三学生200名.如果通过分层抽样的方法从全体高中学生中抽取一个容量为45人的样本,那么应当从三年级的学生中抽取的人数是( )
| A、30 10 5 |
| B、25 15 15 |
| C、20 15 10 |
| D、15 15 15 |