题目内容
6.在△ABC中,角A、B、C所对的边分别为a、b、c,且a=2,cosB=$\frac{3}{5}$.(1)若b=4,求sinA的值;
(2)若△ABC的面积S△ABC=4,求b、c的值.
分析 (1)由cosB=$\frac{3}{5}$>0,且0<B<π,可得sinB=$\sqrt{1-co{s}^{2}B}$.再利用正弦定理即可得出.
(2)由S△ABC=$\frac{1}{2}$acsinB=,解得c,再利用余弦定理即可得出.
解答 解:(1)∵cosB=$\frac{3}{5}$>0,且0<B<π,∴sinB=$\sqrt{1-co{s}^{2}B}$=$\frac{4}{5}$.
由正弦定理得$\frac{a}{sinA}$=$\frac{b}{sinB}$,∴sinA=$\frac{asinB}{b}$=$\frac{2}{4}×\frac{4}{5}$=$\frac{2}{5}$.
(2)∵S△ABC=$\frac{1}{2}$acsinB=$\frac{1}{2}×2c$×$\frac{4}{5}$=4,∴c=5.
由余弦定理得b2=a2+c2-2accosB=22+52-2×2×5×$\frac{3}{5}$=17,∴b=$\sqrt{17}$.
点评 本题考查了三角形面积计算公式、正弦定理余弦定理、同角三角函数基本关系式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
18.某几何体的三视图如图所示,则该几何体的体积为( )


| A. | 8 | B. | $6\sqrt{2}$ | C. | $4\sqrt{2}$ | D. | 4 |
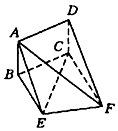 如图,矩形ABCD和梯形BEFC所在平面互相垂直,BE∥CF,∠BCF=∠CEF=90°.AD=$\sqrt{3}$,EF=2
如图,矩形ABCD和梯形BEFC所在平面互相垂直,BE∥CF,∠BCF=∠CEF=90°.AD=$\sqrt{3}$,EF=2