题目内容
1.(1)若角θ的终边过P(-4t,3t)(t>0),求2sinθ+cosθ的值.(2)已知角α的终边上一点P的坐标为($x,-\sqrt{3}$)(x≠0),且$cosα=\frac{{\sqrt{2}}}{4}x$,求sinα和tanα
分析 直接利用三角函数的定义,即可求解.
解答 解:(1)由题意r=5t,∴2sinθ+cosθ=2×$\frac{3t}{5t}$+$\frac{-4t}{5t}$=$\frac{2}{5}$;
(2)∵$cosα=\frac{{\sqrt{2}}}{4}x$,∴$\frac{x}{\sqrt{{x}^{2}+3}}$=$\frac{\sqrt{2}}{4}x$,∴x=$±\sqrt{5}$.
x=$\sqrt{5}$时,sinα=$\frac{-\sqrt{3}}{\sqrt{8}}$=-$\frac{\sqrt{6}}{4}$,tanα=$\frac{-\sqrt{3}}{\sqrt{5}}$=-$\frac{\sqrt{15}}{5}$;
x=-$\sqrt{5}$时,sinα=$\frac{-\sqrt{3}}{\sqrt{8}}$=-$\frac{\sqrt{6}}{4}$,tanα=$\frac{\sqrt{15}}{5}$.
点评 本题考查三角函数的定义,考查学生的计算能力,属于中档题.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
11.某几何体的三视图如图所示,则该几何体的体积为( )
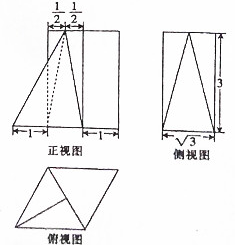

| A. | $4\sqrt{3}$ | B. | $5\sqrt{3}$ | C. | $6\sqrt{3}$ | D. | $8\sqrt{3}$ |
12.若不等式-3≤x2-2ax+a≤-2有唯一解,则a的值是( )
| A. | 2或-1 | B. | $\frac{{-1±\sqrt{5}}}{2}$ | C. | $\frac{{1±\sqrt{5}}}{2}$ | D. | 2 |