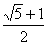题目内容
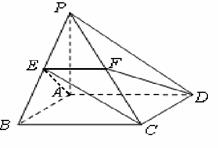
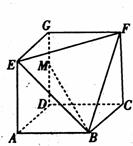
如图,在四棱锥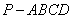 中,底面
中,底面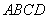 是矩形,
是矩形,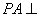 平面
平面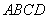 ,
,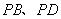 与平面
与平面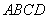 所成角的正切值依次是
所成角的正切值依次是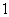 和
和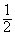 ,
,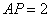 ,
,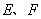 依次是
依次是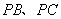 的中点.
的中点.
(1)求证: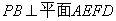 ;
;
(2)求直线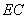 与平面
与平面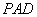 所成角的正弦值.
所成角的正弦值.
(1)∵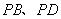 与平面
与平面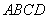 所成角的正切值依次
所成角的正切值依次
是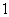 和
和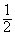 ,
,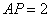 ∴
∴
∵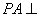 平面
平面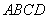 ,底面
,底面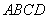 是矩形
是矩形
∴ 平面
平面 ∴
∴
∵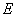 是
是 的中点 ∴
的中点 ∴
∴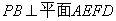
(2)解法一:∵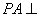 平面
平面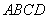 ,∴
,∴ ,又
,又 ,
,
 ∴
∴ 平面
平面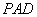 ,取
,取 中点
中点 ,
, 中点
中点 ,联结
,联结 ,
,
则 且
且 ,
, 是平行四边形,
是平行四边形,
∴ 即为直线
即为直线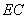 与平面
与平面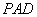 所成的角.
所成的角.
在 中,,
中,, ,
,
 ,
,
∴直线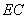 与平面
与平面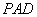 所成角的正弦值为
所成角的正弦值为 .
.
解法二:分别以 为
为 轴、
轴、 轴、
轴、 轴建立空间
轴建立空间
 直角坐标系,依题意,
直角坐标系,依题意, ,则各点坐标分别是
,则各点坐标分别是
 ,
, ,
, ,
, ,
,
 ,∴
,∴ ,
, ,
, ,
,
又∵ 平面
平面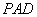 ,
,
∴平面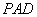 的法向量为
的法向量为 ,
,
设直线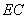 与平面
与平面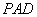 所成的角为
所成的角为 ,则
,则
 ,
,
∴直线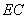 与平面
与平面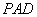 所成角的正弦值为
所成角的正弦值为 .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
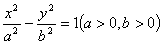 的左顶点与抛物线
的左顶点与抛物线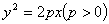 的焦点的距离为4,且双曲线的一条渐近线与抛物线的准线的交点坐标为
的焦点的距离为4,且双曲线的一条渐近线与抛物线的准线的交点坐标为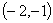 ,则双曲线的焦距为
,则双曲线的焦距为  ,且
,且 与
与 的夹角余弦为
的夹角余弦为 ,则
,则 等于( )
等于( ) B.
B. 或
或

 是两个不同平面,给出四个命题:
是两个不同平面,给出四个命题: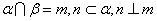 ,则
,则 ②若
②若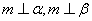 ,则
,则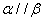
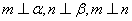 ,则
,则 ,则
,则 ,则满足
,则满足 的
的 的取值范围是
的取值范围是
 满足
满足 ,且
,且 为偶函数,当
为偶函数,当 时,有( )
时,有( ) B.
B. 
 D.
D. 
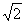 B.
B.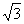 C.
C.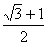 D.
D.