题目内容
16．若直线l：$\frac{x}{a}$+$\frac{y}{b}$=1（a＞0，b＞0）经过点（1，2），则直线l作坐标轴所围成的三角形面积的最小值是4．分析 先求出$\frac{1}{a}$+$\frac{2}{b}$=1，根据基本不等式的性质，求出三角形面积的最小值即可．
解答 解：由题意得：$\frac{1}{a}$+$\frac{2}{b}$=1，又直线l在x轴和y轴的截距分别是a，b，
∴直线l与坐标轴所围成的三角形的面积为S=$\frac{1}{2}$ab，
∴S=$\frac{1}{2}$ab=$\frac{1}{2}$ab（$\frac{1}{a}$+$\frac{2}{b}$）=$\frac{1}{2}$b+a=（$\frac{1}{2}$b+a）（$\frac{1}{a}$+$\frac{2}{b}$）=$\frac{b}{2a}$+1+1+$\frac{2a}{b}$≥2+2$\sqrt{\frac{b}{2a}•\frac{2a}{b}}$=4，
当且仅当$\frac{b}{2a}$=$\frac{2a}{b}$，即b=2a即a=2，b=4时“=”成立，
故S的最小值是：4．
点评 本题考查了直线方程问题，考查基本不等式的性质，是一道基础题．
练习册系列答案
相关题目
12．若四边形ABCD为菱形，则下列等式中成立的是（ ）
| A． | $\overrightarrow{AB}$+$\overrightarrow{BC}$=$\overrightarrow{AC}$ | B． | $\overrightarrow{AB}$+$\overrightarrow{AC}$=$\overrightarrow{BC}$ | C． | $\overrightarrow{AC}$+$\overrightarrow{BA}$=$\overrightarrow{AD}$ | D． | $\overrightarrow{AC}$+$\overrightarrow{AD}$=$\overrightarrow{DC}$ |
4．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的渐近线方程为y=±$\frac{\sqrt{2}}{2}$x，则此双曲线的离心率为（ ）
| A． | $\sqrt{3}$ | B． | $\sqrt{2}$ | C． | $\frac{\sqrt{6}}{2}$ | D． | $\frac{3}{2}$ |
11．已知双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左焦点为F，右顶点为A，虚轴的上端点为B，线段AB与渐近线交于点M，若FM平分∠BFA，则该双曲线的离心率e=（ ）
| A． | 1+$\sqrt{3}$ | B． | 1+$\sqrt{2}$ | C． | $\sqrt{3}$ | D． | $\sqrt{2}$ |
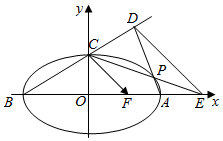如图：A，B，C是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的顶点，点F（c，0）为椭圆的右焦点，原点O到直线CF的距离为$\frac{1}{2}c$，且椭圆过点$（{2\sqrt{3}，1}）$．