题目内容

甲、乙两名同学的乒乓球友谊比赛，实行三局两胜制．已知每局比赛中，若甲先发球，则获胜的概率为
2
3
，否则其获胜的概率为
1
2
．
（Ⅰ）若在第一局比赛中采用掷硬币的方式决定谁先发球，试求甲在此局获胜的概率；
（Ⅱ）若第一局由乙先发球，以后每局由负方先发球．规定：本人发球本人胜一局记1分，对方发球本人胜一局记2分，不论谁发球负一局记0分，记ξ为比赛结束时甲的得分，求随机变量ξ的分布列及数学期望Eξ．
考点：离散型随机变量的期望与方差,离散型随机变量及其分布列
专题：概率与统计
分析：（1）甲获得发球权的概率为
1
2
，如果甲获发球权，则他取胜的概率为
1
2
×
2
3
=
1
3
，若他未获得发球权，则他获胜的概率为
1
2
×
1
2
=
1
4
．由此能求出甲在此局获胜的概率．
（2）由已知得ξ的可能取值为0，1，2，3，4，分别求出相应的概率，由此能求出随机变量ξ的分布列及数学期望Eξ．
解答： 解：（1）甲获得发球权的概率为
1
2
，
如果甲获发球权，则他取胜的概率为
1
2
×
2
3
=
1
3
，
若他未获得发球权，则他获胜的概率为
1
2
×
1
2
=
1
4
．
∴甲在此局获胜的概率P=
1
2
×
2
3
+
1
2
×
1
2
=
1
3
+
1
4
=
7
12
．
（2）由已知得ξ的可能取值为0，1，2，3，4，
ξ=0表示乙连胜两局，P（ξ=0）=
1
2
×
1
3
=
1
6
，
ξ=1表示第一局和第三局乙胜，第二局甲胜，P（ξ=1）=
1
2
×
2
3
×
1
2
=
1
6
，
ξ=2表示第一局甲胜，然后乙连胜两局，P（ξ=2）=
1
2
×
1
2
×
1
3
=
1
12
，
ξ=3表示第一局和第三局甲胜，第二局乙胜或第一局乙胜，然后甲连胜两局，
P（ξ=3）=
1
2
×
1
2
×
2
3
+
1
2
×
2
3
×
1
2
=
1
3
，
ξ=4表示甲连胜两局，P（ξ=4）=
1
2
×
1
2
=
1
4
，
∴ξ的分布列为：
 ξ 0 1 2 3 4
 P 
1
6
 
1
6
 
1
12
 
1
3
 
1
4
∴Eξ=0×
1
6
+1×
1
6
+2×
1
12
+3×
1
3
+4×
1
4
=
7
3
．
点评：本题考查概率的求法，考查离散型随机变量的分布列和数学期望的求法，是中档题，在历年高考中都是必考题型之一．
练习册系列答案
相关题目
已知直线l：y=x与圆C：（x-a）2+y2=1，则“a=
2
”是“直线l与圆C相切”的（　　）
A、充分而不必要条件
B、必要而不充分条件
C、充要条件
D、既不充分又不必要条件
若复数z满足（1+i）z=2-i，则|z|=（　　）
A、
1
2
B、
10
2
C、2
D、
2
2
若命题p：?x0∈R，x02+1＞3x0，则￢p是（　　）
A、?x0∈R，x02+1≤3x0
B、?x∈R，x2+1≤3x
C、?x∈R，x2+1＜3x
D、?x∈R，x2+1＞3x
已知集合A={x|0＜x＜2}，B={x|x-1＞0}，则A∩B=（　　）
A、（1，2）B、（0，1）
C、（0，+∞）D、∅
双曲线
x2
4
-
y2
2
=1的一条渐近线方程为
 
．
双曲线的两条准线将实轴三等分，则它的离心率为（　　）
A、
3
2
B、3
C、
4
3
D、
3
已知函数f（x）=xex的图象在点P（1，e）处的切线与直线x+ky-3=0互相垂直，则k=
 
．
某商店一个月的收支数据为a1，a2，…aN，按程序框图进行统计，那么关于S，T的关系正确的是（　　）
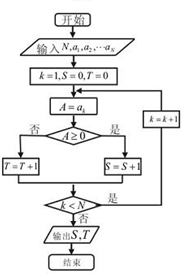
A、N=S-TB、N=S+T
C、S≥TD、S≤T

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网