题目内容
已知公差不为0的等差数列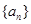 的前3项和
的前3项和 =9,且
=9,且 成等比数列
成等比数列
(1)求数列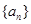 的通项公式和前n项和
的通项公式和前n项和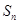 ;
;
(2)设 为数列
为数列 的前n项和,若
的前n项和,若 对一切
对一切 恒成立,求实数
恒成立,求实数 的最小值
的最小值
(1) ;(2)实数
;(2)实数 的最小值为
的最小值为
解析试题分析:(1)求数列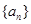 的通项公式和前n项和
的通项公式和前n项和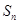 ,因为数列
,因为数列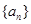 是公差不为0的等差数列,故只需求出
是公差不为0的等差数列,故只需求出 即可,由题意
即可,由题意 =9,且
=9,且 成等比数列,可得
成等比数列,可得 ,即
,即 ,解出
,解出 ,代入
,代入 ,可求出数列
,可求出数列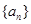 的通项公式和前n项和
的通项公式和前n项和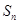 ;(2)求实数
;(2)求实数 的最小值,由题意
的最小值,由题意 为数列
为数列 的前n项和,若
的前n项和,若 对一切
对一切 恒成立,关键是求数列
恒成立,关键是求数列 的通项公式,由(1)可知
的通项公式,由(1)可知 ,可得
,可得 ,从而可得
,从而可得 ,代入
,代入 ,利用基本不等式,即可求出实数
,利用基本不等式,即可求出实数 的最小值
的最小值
试题解析:(1)设 ,
,
由 =9得:
=9得: ①; 2分
①; 2分 成等比数列得:
成等比数列得: ②;联立①②得
②;联立①②得 ; 4分
; 4分
故 6分
6分
(2)∵ 8分
8分
∴ 10分
10分
由 得:
得:
令 ,可知f(n)单调递减,即
,可知f(n)单调递减,即 12分
12分
考点:等差数列的通项公式及前n项和,数列求和

练习册系列答案
相关题目
 的首项
的首项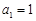 ,
, 是
是 项和,且
项和,且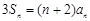
 .
.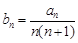 ,求数列
,求数列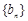 的通项公式;
的通项公式;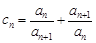 ,证明:
,证明: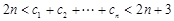 ,
,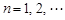 .
.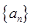 的前
的前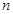 项和
项和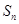 ,且满足
,且满足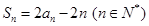 .
.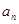 .
.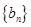 满足
满足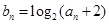 ,
,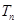 为数列{
为数列{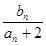 }的前
}的前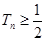 .
. ,
, ,设
,设 是等差数列
是等差数列 的前
的前 项和,若
项和,若 ,且首项
,且首项 是
是 中的最大数,
中的最大数,  .
. 满足
满足 ,求
,求 的值.
的值.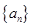 ,其前n项和
,其前n项和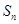 满足
满足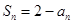 ;等差数列
;等差数列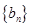 中
中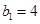 ,且
,且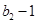 是
是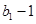 与
与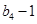 的等比中项
的等比中项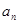 和
和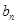 ,
,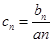 ,求
,求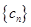 的前n项和
的前n项和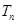 .
. 上两点
上两点 ,若
,若 ,且P点的横坐标为
,且P点的横坐标为 .
. 求
求 ;
; 为数列
为数列 的前n项和,若
的前n项和,若 对一切
对一切 都成立,试求a的取值范围.
都成立,试求a的取值范围. 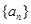 的各项均为正数,其前n项的和为
的各项均为正数,其前n项的和为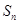 ,对于任意正整数m,n,
,对于任意正整数m,n, 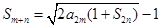 恒成立.
恒成立. 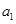 =1,求
=1,求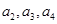 及数列
及数列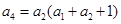 ,求证:数列
,求证:数列 }中,a1=1,
}中,a1=1, 是数列{
是数列{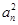 +p
+p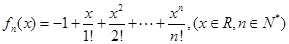
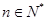 ,存在唯一的
,存在唯一的 ,满足
,满足 ;
;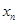 构成数列
构成数列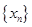 ,判断数列
,判断数列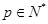 ,
,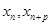 满足(Ⅰ),试比较
满足(Ⅰ),试比较 与
与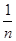 的大小.
的大小.