题目内容
已知数列 的首项
的首项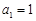 ,
, 是
是 的前
的前 项和,且
项和,且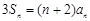
 .
.
(1)若记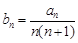 ,求数列
,求数列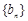 的通项公式;
的通项公式;
(2)记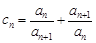 ,证明:
,证明: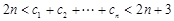 ,
,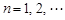 .
.
(1) 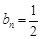 ;(2)详见解析.
;(2)详见解析.
解析试题分析:(1)由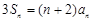 ,得:
,得:
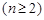 ,两式相加,得:
,两式相加,得: ,
,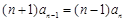
 ,即
,即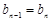 ,所以
,所以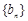 是常数列.又
是常数列.又 ,即可求出结果;(2)由(1)得
,即可求出结果;(2)由(1)得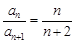 ,进而可求
,进而可求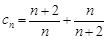 ,又
,又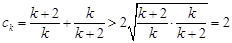 ,所以
,所以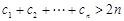 ;又由于
;又由于 ,利于裂项相消法可求得
,利于裂项相消法可求得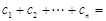
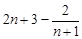
 ,显然可证右边成立.
,显然可证右边成立.
(1)由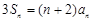 ,得:
,得:
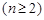 ,
,
两式相加,得: ,
,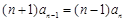

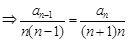 ,即
,即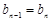 ,所以
,所以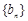 是常数列.
是常数列.
又 ,所以
,所以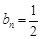 . .5分
. .5分
(2)由(1)得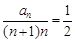 ,从而
,从而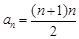 ,
,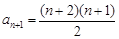 ,
,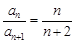 ,
,
故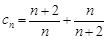 . .7分
. .7分
由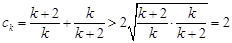 ,所以
,所以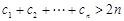 . 9分
. 9分
又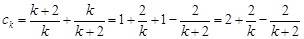 ,
,
所以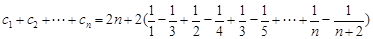


 . .12分
. .12分
(注: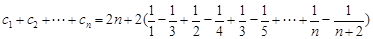

 ,因为
,因为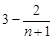
 ,所以
,所以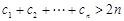 ).
).
考点:1.数列的递推公式;2.数列的前n项和;3.不等式证明.

练习册系列答案
相关题目
 的通项公式为
的通项公式为 ,则数列
,则数列 中数值最大的项是第 项
中数值最大的项是第 项 的前
的前 项和
项和 .
. 满足
满足 ,且
,且 ,求
,求 .
.
 ,其余的人听“美术鉴赏”课;从第二次起,学生可从两个课中自由选择.据往届经验,凡是这一次选择“音乐欣赏”的学生,下一次会有20﹪改选“美术鉴赏”,而选“美术鉴赏”的学生,下次会有30﹪改选“音乐欣赏”,用
,其余的人听“美术鉴赏”课;从第二次起,学生可从两个课中自由选择.据往届经验,凡是这一次选择“音乐欣赏”的学生,下一次会有20﹪改选“美术鉴赏”,而选“美术鉴赏”的学生,下次会有30﹪改选“音乐欣赏”,用 分别表示在第
分别表示在第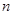 次选“音乐欣赏”课的人数和选“美术鉴赏”课的人数.
次选“音乐欣赏”课的人数和选“美术鉴赏”课的人数. ,分别求出第二次,第三次选“音乐欣赏”课的人数
,分别求出第二次,第三次选“音乐欣赏”课的人数 ;
; 是等比数列,并用
是等比数列,并用 ;
;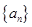 满足:
满足: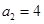 ,公比
,公比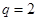 ,数列
,数列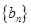 的前
的前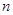 项和为
项和为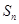 ,且
,且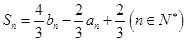 .
.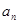 和
和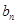 ;
;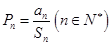 ,证明:
,证明: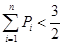 .
. 满足
满足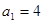 ,
, ,数列
,数列 满足
满足 .
. ,求满足不等式
,求满足不等式 的所有正整数
的所有正整数 的值.
的值.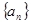 中,若
中,若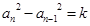 (
(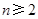 ,
,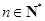 ,
,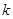 为常数),则称
为常数),则称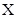 数列.
数列.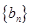 是
是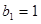 ,
,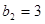 ,写出所有满足条件的数列
,写出所有满足条件的数列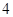 项;
项; 或
或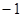 ;
;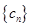 满足
满足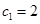 ,
,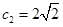 ,
,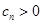 ,设数列
,设数列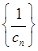 的前
的前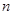 项和为
项和为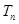 .是否存在
.是否存在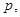
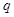 ,使不等式
,使不等式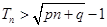 对一切
对一切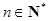 都成立?若存在,求出
都成立?若存在,求出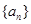 的前3项和
的前3项和 =9,且
=9,且 成等比数列
成等比数列 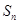 ;
; 为数列
为数列 的前n项和,若
的前n项和,若 对一切
对一切 恒成立,求实数
恒成立,求实数 的最小值
的最小值