题目内容
8.已知|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=2,且$\overrightarrow{a}$$•\overrightarrow{b}$=0,若向量的模|$\overrightarrow{c}$$-\overrightarrow{a}$$+\overrightarrow{b}$|=1,则|$\overrightarrow{c}$|的最小值为$\sqrt{5}$-1.分析 根据平面向量的几何意义,作出图形,找出$\overrightarrow{c}$的终点轨迹,利用几何知识得出最小值.
解答 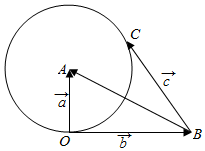 解:设$\overrightarrow{OA}=\overrightarrow{a}$,$\overrightarrow{OB}=\overrightarrow{b}$,$\overrightarrow{BC}=\overrightarrow{c}$.
解:设$\overrightarrow{OA}=\overrightarrow{a}$,$\overrightarrow{OB}=\overrightarrow{b}$,$\overrightarrow{BC}=\overrightarrow{c}$.
∵$\overrightarrow{a}$$•\overrightarrow{b}$=0,∴OA⊥OB,∴AB=$\sqrt{5}$.
∵|$\overrightarrow{c}$$-\overrightarrow{a}$$+\overrightarrow{b}$|=|$\overrightarrow{BC}-\overrightarrow{BA}$|=|$\overrightarrow{AC}$|=1,
∴C的轨迹是以A为圆心,以1为半径的圆.
∴|$\overrightarrow{c}$|的最小值是AB-1=$\sqrt{5}-1$.
故答案为$\sqrt{5}-1$.
点评 本题考查了平面向量的几何意义,属于基础题.

练习册系列答案
相关题目
19.已知变量x与变量y之间具有相关关系,并测得如下一组数据:
则变量x与y之间的线性回归直线方程可能为( )
| x | 6 | 5 | 10 | 12 |
| y | 6 | 5 | 3 | 2 |
| A. | $\widehaty$=0.7x-2.3 | B. | $\widehaty$=-0.7x+10.3 | C. | $\widehaty$=-10.3x+0.7 | D. | $\widehaty$=10.3x-0.7 |
17.函数y=sin2x的图象的一个对称中心为( )
| A. | (0,0) | B. | ($\frac{π}{4}$,0) | C. | ($\frac{π}{4}$,$\frac{1}{2}$) | D. | ($\frac{π}{2}$,1) |