题目内容

1．设$0≤x≤\frac{π}{4}$，则$\sqrt{1-2sinxcosx}$=（　　）
A．cosx-sinxB．sinx-cosxC．cosx+sinxD．-cosx-sinx

分析 由条件求得 cosx＞sinx，再利用同角三角函数的基本关系化简所给的式子，可得结果．

解答 解：设$0≤x≤\frac{π}{4}$，则 cosx＞sinx，则$\sqrt{1-2sinxcosx}$=|cosx-sinx|=cosx-sinx，
故选：A．

点评 本题主要考查同角三角函数的基本关系，判断cosx＞sinx 是解题的关键，属于基础题．

练习册系列答案
相关题目
10．矩形的长为12．宽为8，与它周长相等的正方形的面积是（　　）
A．96B．48C．40D．10
12．已知下列命题：
①有向线段就是向量，向量就是有向线段；
②如果向量$\vec a$与向量$\vec b$平行，则$\vec a$与$\vec b$的方向相同或相反；
③如果向量$\overrightarrow{AB}$与向量$\overrightarrow{CD}$共线，则A，B，C，D四点共线；
④如果$\overrightarrow a$∥$\vec b$，$\vec b$∥$\overrightarrow c$，那么$\overrightarrow a$∥$\overrightarrow c$；
⑤两个向量不能比较大小，但是他们的模能比较大小．
其中正确的命题为（　　）
A．①②④⑤B．②④⑤C．⑤D．③④
9．计算：（$\frac{16}{81}$）${\;}^{-\frac{3}{4}}$+lg$\frac{3}{7}$+lg70+$\sqrt{（lg3）^{2}-lg9+1}$=$\frac{43}{8}$．
16．在△ABC中，角A，B，C的对边分别为a，b，c，且其面积$S=\frac{{{a^2}+{b^2}-{c^2}}}{{4\sqrt{3}}}$，则角C=$\frac{π}{6}$．
6．已知数列{an}满足：a1=1，${2^{n-1}}{a_n}={a_{n-1}}（n∈{N^*}，n≥2）$，则数列{an}的通项公式为an=${（\frac{1}{2}）^{\frac{n（n-1）}{2}}}$．
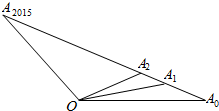13．如图，O为直线A0A2015外一点，若A0，A1，A2，A3，A4，A5，…，A2015中任意相邻两点的距离相等，设$\overrightarrow{O{A}_{0}}$=$\overrightarrow{a}$，$\overrightarrow{O{A}_{2015}}$=$\overrightarrow{b}$，用$\overrightarrow{a}$，$\overrightarrow{b}$表示$\overrightarrow{O{A}_{0}}$+$\overrightarrow{O{A}_{1}}$+…+$\overrightarrow{O{A}_{2015}}$，其结果为1008（$\overrightarrow{a}$+$\overrightarrow{b}$）．
10．设甲乙两地相距100海里，船从甲地匀速驶到乙地，已知某船的最大船速是36海里/时：当船速不大于每小时30海里/时，船每小时使用的燃料费用和船速成正比；当船速不小于每小时30海里/时，船每小时使用的燃料费用和船速的平方成正比；当船速为30海里/时，它每小时使用的燃料费用为300元；其余费用（不论船速为多少）都是每小时480元；
（1）试把每小时使用的燃料费用P（元）表示成船速v（海里/时）的函数；
（2）试把船从甲地行驶到乙地所需要的总费用Y表示成船速v的函数；
（3）当船速为每小时多少海里时，船从甲地到乙地所需要的总费用最少？
11．已知sin（$\frac{π}{6}$-α）-cosα=$\frac{1}{3}$，则cos（2α+$\frac{π}{3}$）=（　　）
A．$\frac{5}{18}$B．-$\frac{5}{18}$C．$\frac{7}{9}$D．-$\frac{7}{9}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网