题目内容
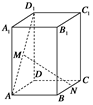
在正四面体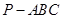 (所有棱长都相等)中,
(所有棱长都相等)中,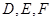 分别是
分别是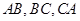 的中点,下面四个结论中不成立的是( )
的中点,下面四个结论中不成立的是( )
A.平面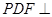 平面 平面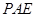 | B.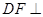 平面 平面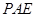 |
C.平面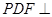 平面 平面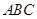 | D.平面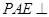 平面 平面 |
C
解析试题分析:由AF⊥BC,PE⊥BC,可得BC⊥平面PAE,而DF//BC,所以,DF⊥平面PAE,故A正确.
若PO⊥平面ABC,垂足为O,则O在AE上,则DF⊥PO,又DF⊥AE,故DF⊥平面PAE,故B正确.
由DF⊥平面PAE可得,平面PAE⊥平面ABC,故D正确.
故选C.
考点:正四面体的几何特征,平行、垂直关系。
点评:中档题,本题在正四面体内,较全面的考查平行、垂直关系,关键是要熟练掌握判定定理及性质定理。

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
设 为直线,
为直线, 是两个不同的平面,下列命题中正确的是( )
是两个不同的平面,下列命题中正确的是( )
A.若 ,则 ,则 | B.若 ,则 ,则 |
C.若 ,则 ,则 | D.若 ,则 ,则 |
已知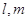 是两条不同的直线,
是两条不同的直线,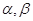 是两个不同的平面,在下列条件中,能成为
是两个不同的平面,在下列条件中,能成为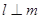 的充分条件的是( )
的充分条件的是( )
A.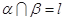 , ,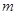 与 与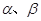 所成角相等 所成角相等 |
B.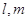 在 在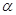 内的射影分别为 内的射影分别为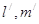 ,且 ,且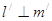 |
C.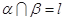 , ,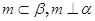 |
D.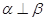 , ,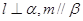 |
已知正四棱柱 中
中 为
为 的中点,则直线
的中点,则直线 与平面
与平面 的距离为( )
的距离为( )
A. | B. | C. | D. |
已知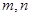 为不同的直线,
为不同的直线,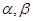 为不同的平面,给出下列四个命题:
为不同的平面,给出下列四个命题:
①若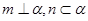 ,则
,则 ; ②若
; ②若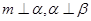 ,则
,则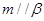 ;
;
③若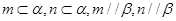 ,则
,则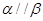 ; ④若
; ④若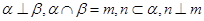 ,则
,则 .
.
其中所有正确命题的序号是( )
| A.①② | B.②③ | C.①③ | D.①④ |
已知点B是点A(3,4,-2)在xOy平面上的射影,则 等于( )
等于( )
| A.(3,4,0) | B. | C. 5 | D. |
已知m,n为两条不同的直线,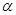 、
、 为两个不同的平面,则下列命题中正确的是
为两个不同的平面,则下列命题中正确的是
A.若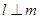  , ,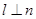  ,且 ,且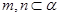  ,则 ,则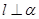  |
B.若平面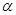  内有不共线的三点到平面 内有不共线的三点到平面  的距离相等,则 的距离相等,则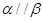  |
C.若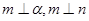  ,则 ,则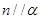  |
D.若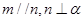  ,则 ,则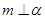 |
设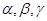 是三个互不重合的平面,m,n是两条不重合的直线,则下列命题中正确的是( )
是三个互不重合的平面,m,n是两条不重合的直线,则下列命题中正确的是( )
A. | B.若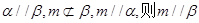 |
C.若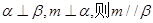 | D.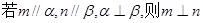 |
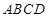 -
-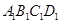 ,
,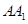 =2,
=2,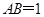 ,
,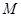 ,
,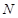 分别在
分别在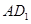 ,
,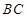 上移动,且始终保持
上移动,且始终保持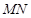 ∥平面
∥平面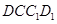 ,设
,设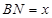 ,
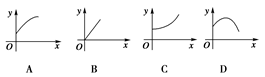
,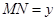 ,则函数
,则函数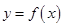 的图象大致是( )
的图象大致是( )