题目内容
已知正四棱柱 中
中 为
为 的中点,则直线
的中点,则直线 与平面
与平面 的距离为( )
的距离为( )
A. | B. | C. | D. |
D
解析试题分析:如图:连接AC,交BD于O,在三角形CC1A中,易证OE∥C1A,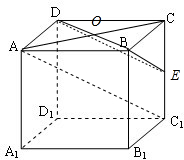
从而C1A∥平面BDE,∴直线AC1与平面BED的距离即为点A到平面BED的距离,设为h.
在三棱锥E-ABD中,VE-ABD=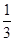 S△ABD×EC=
S△ABD×EC=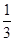 ×
×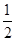 ×2×2
×2×2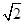 =
=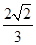 .
.
在三棱锥A-BDE中,BD=2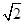 ,BE=
,BE= ,DE=
,DE= ,∴S△EBD=
,∴S△EBD=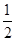 ×2
×2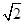 ×2=2
×2=2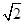 .
.
∴VA-BDE=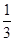 ×S△EBD×h=
×S△EBD×h=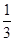 ×2
×2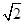 ×h=
×h=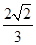 ,∴h=1,
,∴h=1,
故选 D.
考点:正四棱柱的几何特征,距离计算。
点评:中档题,涉及立体几何中距离计算问题,要充分借助于几何体的特征,并注意距离的“转化”。本题利用“体积法”计算距离,值得学习。

练习册系列答案
相关题目
关于空间两条直线 、
、 与平面
与平面 ,下列命题正确的是( )
,下列命题正确的是( )
A.若 ,则 ,则 | B.若 ,则 ,则 |
C. ,则 ,则 | D.若 则 则 |
对于平面 、
、 、
、 和直线
和直线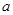 、
、 、
、 、
、 ,下列命题中真命题是 ( )
,下列命题中真命题是 ( )
A.若 ,则 ,则 ; ; |
B.若 则 则 ; ; |
C.若 ,则 ,则 ; ; |
D.若 ,则 ,则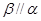 . . |
已知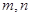 为异面直线,
为异面直线,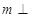 平面
平面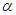 ,
,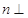 平面
平面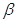 .直线
.直线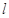 满足
满足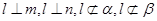 ,则( )
,则( )
A.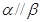 ,且 ,且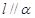 |
B.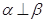 ,且 ,且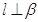 |
C.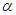 与 与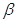 相交,且交线垂直于 相交,且交线垂直于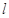 |
D.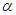 与 与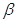 相交,且交线平行于 相交,且交线平行于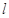 |
关于直线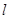 ,
, 及平面
及平面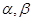 ,下列命题中正确的是( )
,下列命题中正确的是( )
A.若l∥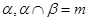 ,则l∥m ,则l∥m | B.若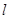 ∥ ∥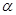 ,m∥ ,m∥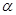 ,则 ,则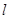 ∥m ∥m |
C.若l⊥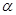 ,l∥ ,l∥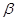 ,则 ,则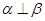 | D.若l∥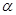 ,m⊥l,则m⊥ ,m⊥l,则m⊥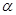 |
对于不重合的直线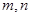 和不重合的平面
和不重合的平面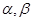 ,下列命题错误的是( )
,下列命题错误的是( )
A.若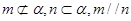 ,则 ,则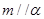 | B.若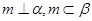 ,则 ,则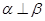 |
C.若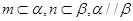 ,则 ,则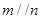 | D.若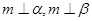 ,则 ,则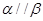 |
在正四面体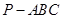 (所有棱长都相等)中,
(所有棱长都相等)中,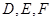 分别是
分别是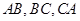 的中点,下面四个结论中不成立的是( )
的中点,下面四个结论中不成立的是( )
A.平面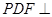 平面 平面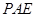 | B.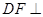 平面 平面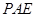 |
C.平面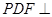 平面 平面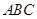 | D.平面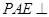 平面 平面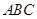 |
对于平面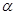 与共面的直线m,n,下列命题为真命题的是 ( )
与共面的直线m,n,下列命题为真命题的是 ( )
A.若m,n与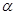 所成的角相等,则m//n 所成的角相等,则m//n | B.若m//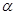 ,n// ,n//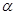 ,则m//n ,则m//n |
C.若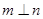 , ,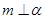 ,则 ,则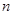 // //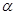 | D.若m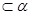 ,n// ,n//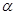 ,则m//n ,则m//n |
如图,正方体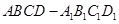 的棱长为1,线段
的棱长为1,线段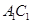 上有两个动点
上有两个动点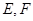 ,且
,且 ;则下列结论错误的是( )
;则下列结论错误的是( )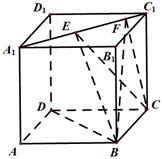
A.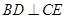 |
B.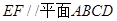 |
C.三棱锥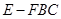 的体积为定值 的体积为定值 |
D.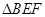 的面积与 的面积与 的面积相等 的面积相等 |