题目内容
如图,正四棱柱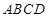 -
-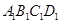 ,
,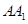 =2,
=2,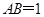 ,
,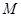 ,
,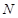 分别在
分别在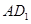 ,
,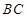 上移动,且始终保持
上移动,且始终保持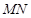 ∥平面
∥平面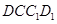 ,设
,设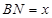 ,
,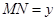 ,则函数
,则函数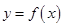 的图象大致是( )
的图象大致是( )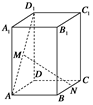
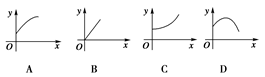
C
解析试题分析:作 ,连接NH,由于
,连接NH,由于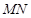 ∥平面
∥平面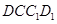 ,则
,则 。由于
。由于 ,求得
,求得 。又因为
。又因为 ,
,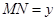 ,所以
,所以 ,
, ,化为
,化为 ,其图像是C。
,其图像是C。
考点:函数的图象与图象变化;直线与平面平行的性质
点评:本题考查的知识点是线面平行的性质,函数的图象与性质等,根据已知列出函数的解析式是解答本题的关键.

练习册系列答案
相关题目
关于直线 以及平面
以及平面 ,给出下列命题:
,给出下列命题:
①若 ,
, ,则
,则
②若 ,
, ,则
,则
③若 且
且 ,则
,则
④若 则
则
其中正确的命题是( )
| A.①② | B.②③ | C.②④ | D.①④ |
已知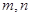 为异面直线,
为异面直线,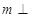 平面
平面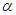 ,
,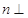 平面
平面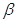 .直线
.直线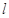 满足
满足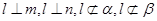 ,则( )
,则( )
A.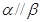 ,且 ,且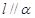 |
B.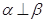 ,且 ,且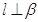 |
C.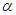 与 与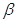 相交,且交线垂直于 相交,且交线垂直于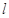 |
D.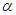 与 与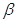 相交,且交线平行于 相交,且交线平行于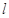 |
对于不重合的直线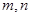 和不重合的平面
和不重合的平面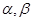 ,下列命题错误的是( )
,下列命题错误的是( )
A.若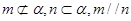 ,则 ,则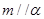 | B.若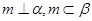 ,则 ,则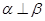 |
C.若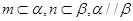 ,则 ,则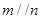 | D.若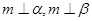 ,则 ,则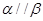 |
在正四面体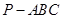 (所有棱长都相等)中,
(所有棱长都相等)中,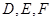 分别是
分别是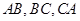 的中点,下面四个结论中不成立的是( )
的中点,下面四个结论中不成立的是( )
A.平面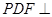 平面 平面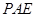 | B.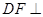 平面 平面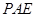 |
C.平面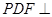 平面 平面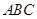 | D.平面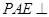 平面 平面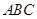 |
对于直线 ,
, 和平面
和平面 ,
, ,使
,使 成立的一个充分条件是
成立的一个充分条件是
A. , , ∥ ∥ | B. ∥ ∥ , , |
C. , , , , | D. , , , , |
对于平面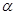 与共面的直线m,n,下列命题为真命题的是 ( )
与共面的直线m,n,下列命题为真命题的是 ( )
A.若m,n与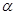 所成的角相等,则m//n 所成的角相等,则m//n | B.若m//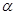 ,n// ,n//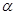 ,则m//n ,则m//n |
C.若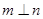 , ,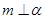 ,则 ,则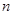 // //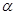 | D.若m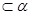 ,n// ,n//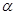 ,则m//n ,则m//n |
若 是空间三条不同的直线,
是空间三条不同的直线, 是空间中不同的平面,则下列命题中不正确的是( )
是空间中不同的平面,则下列命题中不正确的是( )
A.若 , , ,则 ,则 |
B.若 , , ,则 ,则 |
C.当 且 且 是 是 在 在 内的射影,若 内的射影,若 ,则 ,则 |
D.当 且 且 时,若 时,若 ,则 ,则 |
