题目内容
在实数集R中，我们定义的大小关系“＞”为全体实数排了一个“序”类似的，我们在平面向量集D={
|
=（x，y），x∈R，y∈R}上也可以定义在一个称“序”的关系，记为“＞＞”，定义如下：对于任意两个向量
=（x1，y1）
2=（x2，y2），“
1＞＞
2”当且仅当“x1＞x2”或“x1=x2”且“y1＞y2”，按上述定义的关系“＞＞”给出如下四个命题：
①若
1=（1，0），
2=（0，1），
=（0，0），则
1＞＞
2＞＞
②若
1＞＞
2，
2＞＞
3，则
1＞＞
3
③若
1＞＞
2，则对于任意
∈D，
1+
＞＞
2+
④对于任意向量
＞＞
，
=（0，0），若
1＞＞
2，则
•
1=
•
2
其中真命题的序号为 ．
| a |
| a |
| a1 |
| a |
| a |
| a |
①若
| e |
| e |
| 0 |
| e |
| e |
| 0 |
②若
| a |
| a |
| a |
| a |
| a |
| a |
③若
| a |
| a |
| a |
| a |
| a |
| a |
| a |
④对于任意向量
| a |
| 0 |
| 0 |
| a |
| a |
| a |
| a |
| a |
| a |
其中真命题的序号为
考点：命题的真假判断与应用
专题：平面向量及应用,简易逻辑
分析：①由
=（1，0），
=（0，1），横坐标1＞0，可得
＞＞
，而
=（0，0），横坐标0=0，纵坐标1＞0，即可判断
＞＞
＞＞
；
②若
＞＞
，则“x1＞x2”或“x1=x2”且“y1＞y2”，若
＞＞
，则“x2＞x3”或“x2=x3”且“y2＞y3”，利用不等式的性质即可判断出正误；
③若
＞＞
，则“x1＞x2”或“x1=x2”且“y1＞y2”，对于任意
=（x，y）∈D，利用不等式的性质可得x1+x＞x2+x，或x1+x=x2+x且y1+y＞y2+y，
即可判断出正误；
④对于任意向量
＞＞
，
=（0，0），若
＞＞
，取
=（4，3），
=（2，1），
=（1，1），利用数量积运算可得：
•
=7，
•
=3，
•
≠
•
，即可判断出正误．
| e1 |
| e2 |
| e1 |
| e2 |
| 0 |
| e1 |
| e2 |
| 0 |
②若
| a1 |
| a2 |
| a2 |
| a3 |
③若
| a1 |
| a2 |
| a |
即可判断出正误；
④对于任意向量
| a |
| 0 |
| 0 |
| a1 |
| a2 |
| a1 |
| a2 |
| a |
| a |
| a1 |
| a |
| a2 |
| a |
| a1 |
| a |
| a2 |
解答：
解：①∵
=（1，0），
=（0，1），横坐标1＞0，∴
＞＞
，而
=（0，0），横坐标0=0，纵坐标1＞0，则
＞＞
＞＞
；
②若
＞＞
，则“x1＞x2”或“x1=x2”且“y1＞y2”，若
＞＞
，则“x2＞x3”或“x2=x3”且“y2＞y3”，可得“x1＞x3”或“x1=x3，y1＞y3”，则
＞＞
．因此正确．
③若
＞＞
，则“x1＞x2”或“x1=x2”且“y1＞y2”，对于任意
=（x，y）∈D，则x1+x＞x2+x，或x1+x=x2+x且y1+y＞y2+y，因此
+
＞＞
+
．
因此正确；
④对于任意向量
＞＞
，
=（0，0），若
＞＞
，取
=（4，3），
=（2，1），
=（1，1），则
•
=7，
•
=3，因此
•
≠
•
，不正确．
其中真命题的序号为 ①②③．
故答案为：①②③．
| e1 |
| e2 |
| e1 |
| e2 |
| 0 |
| e1 |
| e2 |
| 0 |
②若
| a1 |
| a2 |
| a2 |
| a3 |
| a1 |
| a3 |
③若
| a1 |
| a2 |
| a |
| a1 |
| a |
| a2 |
| a |
因此正确；
④对于任意向量
| a |
| 0 |
| 0 |
| a1 |
| a2 |
| a1 |
| a2 |
| a |
| a |
| a1 |
| a |
| a2 |
| a |
| a1 |
| a |
| a2 |
其中真命题的序号为 ①②③．
故答案为：①②③．
点评：本题考查了新定义、向量的运算、实数的性质、不等式的基本性质，考查了推理能力与计算能力，属于中档题．
练习册系列答案
科学实验活动册系列答案
相关题目
已知直线ax+by=0与双曲线
-
=1（0＜a＜b）交于A，B两点，若A（x1，y1），B（x2，y2）满足|x1-x2|=3
，且|AB|=6，则双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
A、
| ||
| B、3 | ||
C、
| ||
| D、2 |
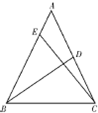如图，在等腰三角形ABC中，底边BC=2，| AD |
| DC |
| AE |
| 1 |
| 2 |
| EB |
| BD |
| AC |
| 1 |
| 2 |
| CE |
| AB |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
运行如图所示的程序框图后，输出的结果是（ ）
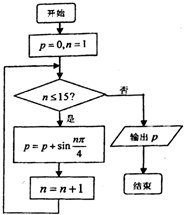
| A、0 | ||||
| B、1 | ||||
C、1+
| ||||
D、1+
|
已知
、
的夹角为120°，且|
|=1，|2
+
|=2
，则|
|=（ ）
| a |
| b |
| a |
| a |
| b |
| 3 |
| b |
A、3
| ||
B、2
| ||
| C、4 | ||
| D、2 |
