题目内容
已知b>-1,c>0,函数f(x)=x+b的图象与函数g(x)=x2+bx+c 的图象相切,
(Ⅰ)求b与c的关系式(用c表示b);
(Ⅱ)设函数F(x)=f(x)g(x)在(-∞,+∞)内有极值点,求c的取值范围。
(Ⅰ)求b与c的关系式(用c表示b);
(Ⅱ)设函数F(x)=f(x)g(x)在(-∞,+∞)内有极值点,求c的取值范围。
解:(Ⅰ)依题意,令f′(x)=g′(x),得2x+b=1,故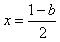 ,
,
由于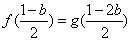 ,得
,得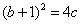 ,
,
∵b>-1,c>0,
∴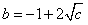 。
。
(Ⅱ)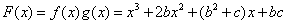 ,
,
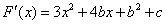 ,
,
令F′(x)=0,即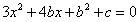 ,
,
则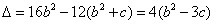 ,
,
若△=0,则F′(x)=0有一个实根x,且F′(x)的变化如下:
于是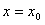 不是函数F(x)的极值点;
不是函数F(x)的极值点;
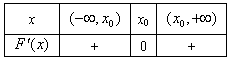
若△>0,则F′(x)=0有两个不相等的实根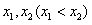 ,且F′(x)的变化如下:
,且F′(x)的变化如下:

由此,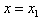 是函数F(x)的极大值点,
是函数F(x)的极大值点,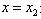 是函数F(x)的极小值点,
是函数F(x)的极小值点,
综上所述,当且仅当△=0时,函数F(x)在(-∞,+∞)内有极值点,
由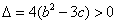 得
得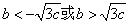 ,
,
∵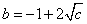 ,
,
∴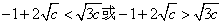 ,解之得
,解之得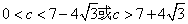 ,
,
故所求c的取值范围是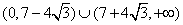 。
。
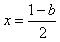 ,
,由于
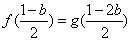 ,得
,得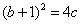 ,
,∵b>-1,c>0,
∴
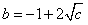 。
。(Ⅱ)
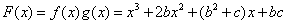 ,
,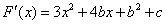 ,
,令F′(x)=0,即
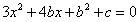 ,
,则
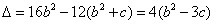 ,
,若△=0,则F′(x)=0有一个实根x,且F′(x)的变化如下:

于是
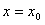 不是函数F(x)的极值点;
不是函数F(x)的极值点;若△>0,则F′(x)=0有两个不相等的实根
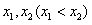 ,且F′(x)的变化如下:
,且F′(x)的变化如下:
由此,
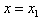 是函数F(x)的极大值点,
是函数F(x)的极大值点,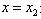 是函数F(x)的极小值点,
是函数F(x)的极小值点,综上所述,当且仅当△=0时,函数F(x)在(-∞,+∞)内有极值点,
由
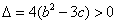 得
得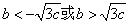 ,
,∵
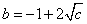 ,
,∴
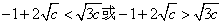 ,解之得
,解之得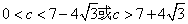 ,
,故所求c的取值范围是
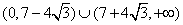 。
。 
练习册系列答案
相关题目