题目内容
设f(x)=6cos2x-2
sinxcosx.
(Ⅰ)求f(x)的最小正周期及单调递增区间;
(Ⅱ)将函数f(x)的图象向右平移
个单位,得y=g(x)的图象,求F(x)=
在x=
处的切线方程.
| 3 |
(Ⅰ)求f(x)的最小正周期及单调递增区间;
(Ⅱ)将函数f(x)的图象向右平移
| π |
| 3 |
| g(x)-3 | ||
2
|
| π |
| 4 |
分析:(Ⅰ)先利用二倍角公式和两角和的余弦公式将函数化为y=Acos(ωx+φ)型函数,再利用周期公式求函数的最小正周期,利用余弦函数图象性质,通过解不等式可得函数的单调增区间
(Ⅱ)先由函数的图象变换法则得函数y=g(x)的解析式,从而确定函数F(x)的解析式,再求函数F(x)的导函数F′(x),最后由导数的几何意义求出F(x)在x=
处的切线斜率,即可得切线方程
(Ⅱ)先由函数的图象变换法则得函数y=g(x)的解析式,从而确定函数F(x)的解析式,再求函数F(x)的导函数F′(x),最后由导数的几何意义求出F(x)在x=
| π |
| 4 |
解答:解:(Ⅰ)f(x)=6
-
sin2x=2
cos(2x+
)+3,
故f(x)的最小正周期T=π
由-π+2kπ≤2x+
≤2kπ得f(x)的单调递增区间为[kπ-
,kπ-
](k∈Z).
(Ⅱ)由题意:g(x)=2
cos[2(x-
)+
]+3=2
sin2x+3,
∴F(x)=
=
,F′(x)=
,
因此切线斜率k=F′(
)=-
,
切点坐标为(
,
),
故所求切线方程为y-
=-
(x-
),
即16x+π2y-8π=0.
| (1+cos2x) |
| 2 |
| 3 |
| 3 |
| π |
| 6 |
故f(x)的最小正周期T=π
由-π+2kπ≤2x+
| π |
| 6 |
| 7π |
| 12 |
| π |
| 12 |
(Ⅱ)由题意:g(x)=2
| 3 |
| π |
| 3 |
| π |
| 6 |
| 3 |
∴F(x)=
| g(x)-3 | ||
2
|
| sin2x |
| x |
| 2xcos2x-sin2x |
| x2 |
因此切线斜率k=F′(
| π |
| 4 |
| 16 |
| π2 |
切点坐标为(
| π |
| 4 |
| 4 |
| π |
故所求切线方程为y-
| 4 |
| π |
| 16 |
| π2 |
| π |
| 4 |
即16x+π2y-8π=0.
点评:本题考察了二倍角公式,两角和的余弦公式,三角函数的图象和性质,导数的四则运算,导数的几何意义等基础知识

练习册系列答案
相关题目
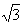 sin2x,
sin2x, ,求tan
,求tan α的值。
α的值。