题目内容
设f(x)=6cos2x-2
sinxcosx；
（Ⅰ）求f（x）的单调递增区间；
（Ⅱ）在△ABC中，角A，B，C的对边分别为a，b，c，锐角A满足f(A)=3-2
，B=
，求
的值．
| 3 |
（Ⅰ）求f（x）的单调递增区间；
（Ⅱ）在△ABC中，角A，B，C的对边分别为a，b，c，锐角A满足f(A)=3-2
| 3 |
| π |
| 12 |
| a2+b2+c2 |
| ab |
分析：（Ⅰ）利用三角函数中的恒等变换可求得f（x）=-2
sin（2x-
）+3，从而可求f（x）的单调递增区间；
（Ⅱ）由（Ⅰ）知f（x）=-2
sin（2x-
）+3，于是f（A）=3-2
⇒sin（2A-
）=1，从而可求得A=
，C=
，利用正弦定理与余弦定理的结合可求得
的值．
| 3 |
| π |
| 3 |
（Ⅱ）由（Ⅰ）知f（x）=-2
| 3 |
| π |
| 3 |
| 3 |
| π |
| 3 |
| 5π |
| 12 |
| π |
| 2 |
| a2+b2+c2 |
| ab |
解答：解：（Ⅰ）∵f（x）=6cos2x-2
sinxcosx
=3（1+cos2x）-
sin2x
=-2
sin（2x-
）+3，
令
+2kπ≤2x-
≤
+2kπ（k∈Z），
得：
+kπ≤x≤
+kπ（k∈Z），
∴f（x）的单调递增区间为[
+kπ，
+kπ]（k∈Z）；
（Ⅱ）∵f（A）=-2
sin（2A-
）+3=3-2
，
∴sin（2A-
）=1，又A为三角形中的内角，
∴A=
，又B=
，
∴C=π-（A+B）=
，
∴
=
=
=
=
=
=8．
| 3 |
=3（1+cos2x）-
| 3 |
=-2
| 3 |
| π |
| 3 |
令
| π |
| 2 |
| π |
| 3 |
| 3π |
| 2 |
得：
| 5π |
| 12 |
| 11π |
| 12 |
∴f（x）的单调递增区间为[
| 5π |
| 12 |
| 11π |
| 12 |
（Ⅱ）∵f（A）=-2
| 3 |
| π |
| 3 |
| 3 |
∴sin（2A-
| π |
| 3 |
∴A=
| 5π |
| 12 |
| π |
| 12 |
∴C=π-（A+B）=
| π |
| 2 |
∴
| a2+b2+c2 |
| ab |
| 2c2 |
| ab |
| 2(sinc)2 |
| sinAsinB |
| 2×1 |
| cosBsinB |
| 2 | ||
|
| 4 | ||
sin
|
点评：本题考查三角函数中的恒等变换，着重考查正弦函数的单调性与正弦定理与余弦定理的综合应用，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
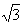sin2x，
，求tan
α的值。