题目内容
15.已知函数f(x)=x-alnx(a∈R)(1)讨论函数f(x)的单调性;
(2)若不等式f(x)≥0恒成立,求a的取值范围.
分析 (1)求出导函数,通过当a≤0时,当a>0时,判断导函数的符号,然后判断函数的单调性.
(2)通过当a=0时,当a<0时,当a>0时,分别求解判断求解函数的最小值,推出a的取值范围.
解答 解:(1)$f'(x)=1-\frac{a}{x}=\frac{x-a}{x}$,…(1分)
当a≤0时,∵x>0,∴f'(x)>0恒成立,
∴f(x)在定义域(0,+∞)上单调递增…(3分)
当a>0时,令f'(x)=0,得x=a,
∵x>0,∴f'(x)>0得x>a;f'(x)<0得0<x<a,
∴f(x)在(0,a)上单调递减,
在(a,+∞)上单调递增.…(5分)
(2)当a=0时,f(x)>0恒成立…(6分)
当a<0时,当x→0时,f(x)→-∞,f(x)≥0不成立…(8分)
当a>0时,由(1)可知f(x)min=f(a)=a-alna,由f(a)=a-alna≥0
得1-lna≥0,∴a∈(0,e]…(11分)
综上所述,a的取值范围是[0,e].…(12分)
点评 本题考查函数的单调性的判断与应用,导数的应用,考查分类讨论思想以及转化思想的应用.

练习册系列答案
相关题目
1.已知复数z=$\frac{4-3i}{6+8i}$(i是虚数单位),则|z|=( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{7}{48}$ | D. | $\frac{3}{10}$ |
6.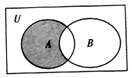 若全集U、集合A、集合B及其关系用韦恩图表示如图所示,则图中阴影表示的集合为( )
若全集U、集合A、集合B及其关系用韦恩图表示如图所示,则图中阴影表示的集合为( )
 若全集U、集合A、集合B及其关系用韦恩图表示如图所示,则图中阴影表示的集合为( )
若全集U、集合A、集合B及其关系用韦恩图表示如图所示,则图中阴影表示的集合为( )| A. | ∁U(A∩B) | B. | ∁U(A∪B) | C. | A∩(∁UB) | D. | (∁UA)∩B |
3.若点A(x,1),B(2,y)均在第一象限,且$\overrightarrow{OA}$•$\overrightarrow{OB}$=1,则$\frac{1}{x}$+$\frac{2}{y}$的最小值为(( )
| A. | 2 | B. | 4 | C. | 8 | D. | 10 |
10.已知函数y=f(x)是定义在R上以π为周期的奇函数,且当x∈[-$\frac{π}{2}$,0)时,f(x)=sinx,则f(-$\frac{5π}{3}$)=( )
| A. | -$\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
20.经过平面α外两点,作与α平行的平面,则这样的平面可以作( )
| A. | 1个或2个 | B. | 0个或1个 | C. | 1个 | D. | 0个 |
4.执行如图所示的程序框图,若输入m=3,n=4,则输出a=( )


| A. | 4 | B. | 8 | C. | 12 | D. | 16 |