题目内容
11.函数y=$\sqrt{2x-3}$+$\frac{1}{x-3}$的定义域为( )| A. | [$\frac{3}{2}$,+∞) | B. | (-∞,3)∪(3,+∞) | C. | [$\frac{3}{2}$,3)∪(3,+∞) | D. | (3,+∞) |
分析 根据函数y的解析式,列出使解析式有意义的不等式组,求出解集即可.
解答 解:函数y=$\sqrt{2x-3}$+$\frac{1}{x-3}$,
∴$\left\{\begin{array}{l}{2x-3≥0}\\{x-3≠0}\end{array}\right.$,
解得x≥$\frac{3}{2}$且x≠3;
∴函数y的定义域为[$\frac{3}{2}$,3)∪(3,+∞).
故选:C.
点评 本题考查了根据函数解析式求定义域的应用问题,是基础题.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
2.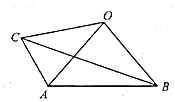 如图,在四边形ABOC中,AO=BO=CO,AB=2,AC=1,∠BAC=120°,若$\overrightarrow{AO}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$,则λ+μ的值为( )
如图,在四边形ABOC中,AO=BO=CO,AB=2,AC=1,∠BAC=120°,若$\overrightarrow{AO}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$,则λ+μ的值为( )
 如图,在四边形ABOC中,AO=BO=CO,AB=2,AC=1,∠BAC=120°,若$\overrightarrow{AO}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$,则λ+μ的值为( )
如图,在四边形ABOC中,AO=BO=CO,AB=2,AC=1,∠BAC=120°,若$\overrightarrow{AO}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$,则λ+μ的值为( )| A. | $\frac{13}{6}$ | B. | $\frac{8}{3}$ | C. | $\frac{17}{6}$ | D. | $\frac{13}{3}$ |
6.已知$sin({α+\frac{π}{6}})=\frac{4}{5}$,则$cos({α-\frac{π}{3}})$的值为( )
| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $-\frac{4}{5}$ | D. | $-\frac{3}{5}$ |
16.已知集合A={x|$\frac{x-10}{x-1}$≤0},B={y|y=lgx,x∈A},则A∪B=( )
| A. | {1} | B. | ∅ | C. | [0,10] | D. | (0,10] |
20.已知i是虚数单位,则复数$z={({\frac{1+i}{{\sqrt{2}}}})^{2017}}$在复平面内对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
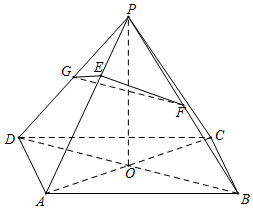 四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠DAB=$\frac{2π}{3}$,AC∩BD=O,且PO⊥平面ABCD,PO=$\sqrt{3}$,点F,G分别是线段PB,PD上的中点,E在PA上,且PA=3PE.
四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠DAB=$\frac{2π}{3}$,AC∩BD=O,且PO⊥平面ABCD,PO=$\sqrt{3}$,点F,G分别是线段PB,PD上的中点,E在PA上,且PA=3PE.