题目内容
已知函数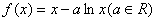 .
.
(1)设函数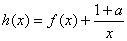 ,求函数
,求函数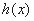 的单调区间;
的单调区间;
(2)若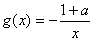 ,在
,在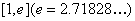 上存在一点
上存在一点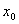 ,使得
,使得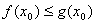 成立,求
成立,求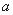 的取值范围.
的取值范围.
(1) ,定义域为
,定义域为 ,
,
 1分
1分
①当 ,即
,即 时,令
时,令 ,
,
令 ,
, 2分
2分
②当 ,即
,即 时,
时, 恒成立, 3分
恒成立, 3分
综上:当 时,
时, 在
在 上单调递减,在
上单调递减,在 上单调递增.
上单调递增.
当 时,
时, 在
在 上单调递增. 4分
上单调递增. 4分
(2)由题意可知,在 上存在一点
上存在一点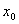 ,使得
,使得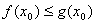 成立,
成立,
即在 上存在一点
上存在一点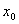 ,使得
,使得 ,
,
即函数 在
在 上的最小值
上的最小值 . 5分
. 5分
由第(2)问,①当 ,即
,即 时,
时, 在
在 上单调递减,
上单调递减,
 ,
, ,
,
 ,
, ; 7分
; 7分
②当 ,即
,即 时,
时, 在
在 上单调递增,
上单调递增,
 ,
, 9分
9分
③当 ,即
,即 时,
时,

 ,
, ,
,
此时不存在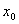 使
使 成立. 11分
成立. 11分
综上可得所求 的范围是:
的范围是: 或
或 .
.

练习册系列答案
相关题目
已知扇形的面积为2 cm2 ,扇形圆心角的弧度数是4,则扇形的周长为( )
,扇形圆心角的弧度数是4,则扇形的周长为( )
|
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
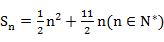 .
.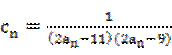 ,数列{cn}的前n项和为Tn,求使不等式Tn>
,数列{cn}的前n项和为Tn,求使不等式Tn>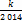 对一切n∈N*都成立的最大正整数k的值;
对一切n∈N*都成立的最大正整数k的值;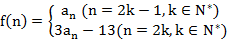 ,是否存在m∈N*,使得f(m+15)=5f(m)成立?若存在,求出m的值;若不存在,请说明理由.
,是否存在m∈N*,使得f(m+15)=5f(m)成立?若存在,求出m的值;若不存在,请说明理由.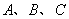 是
是 的三个内角,
的三个内角, 是各角的对边,
是各角的对边,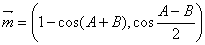 ,
,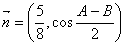 ,且
,且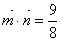 .
.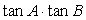 的值;
的值;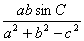 的最大值.
的最大值. 是定义域为R的奇函数,且
是定义域为R的奇函数,且 ,
, 的图象如图所示。若正数
的图象如图所示。若正数 ,则
,则 的取值范围是( )
的取值范围是( ) A.
A. B.
B. C.
C. D.
D.
 >0,求证:
>0,求证: ≥
≥
 中至少有一个小于2。
中至少有一个小于2。 ,则可归纳出
,则可归纳出 =( )
=( ) B.
B. C.
C. D.
D.
 .若
.若 有5个不同的零点,则实数
有5个不同的零点,则实数 的取值范围为( )
的取值范围为( ) B.
B. C.
C. D.
D.
 B.
B.  C.
C.  D.
D. 
