题目内容
(1) 设 ≥
≥ >0,求证:
>0,求证: ≥
≥
(2)已知 中至少有一个小于2。
中至少有一个小于2。
【解析】
试题分析:【1】先作差然后利用综合法的思想证明即可。
因为 ≥
≥ >0,所以
>0,所以 ≥0,
≥0, >0,从而
>0,从而 ≥0,
≥0,
即 ≥
≥
【2】证明:假设 都不小于2,则
都不小于2,则
因为 ,所以
,所以 ,
, 即
即 ,
,
这与已知 相矛盾,故假设不成立。综上
相矛盾,故假设不成立。综上 中至少有一个小于2。
中至少有一个小于2。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
为了解72名学生的学习情况,采用系统抽样的 方法,从中抽取容量为8的样本,则分段的间隔为( )
方法,从中抽取容量为8的样本,则分段的间隔为( )
|
| A. | 10 | B. | 8 | C. | 9 | D. | 7 |
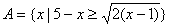 ,
, ,当“x
,当“x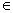
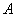 ” 是“x
” 是“x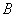 ”的充分不必要条件,则
”的充分不必要条件,则 的取值范围是 .
的取值范围是 .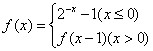 ,若方程
,若方程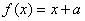 有且只有两个不相等
有且只有两个不相等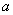 的取值范围是( )
的取值范围是( ) 的图象如下图所示,则导函数
的图象如下图所示,则导函数 的图象的大致形状是( )
的图象的大致形状是( )

 上的函数
上的函数 ,
, 是它的导函数,且恒有
是它的导函数,且恒有 成立,则 A.
成立,则 A. B.
B.
 D.
D.
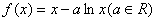 .
.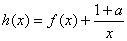 ,求函数
,求函数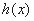 的单调区间;
的单调区间; 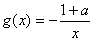 ,在
,在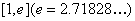 上存在一点
上存在一点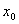 ,使得
,使得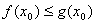 成立,求
成立,求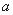 的取值范围.
的取值范围. ,则
,则 的值为( )
的值为( ) B.
B.
 中较小的数 D.
中较小的数 D. ,
, ,则
,则 中元素的个数为
中元素的个数为