题目内容
5．函数g（x）=$\frac{a}{x+2}$在[1，2]上为减函数，则a的取值范围为（ ）| A． | （-∞，0） | B． | [0，+∞） | C． | （0，+∞） | D． | （-∞，0] |
分析 由条件可得当x∈[1，2]时，y′=$\frac{-a}{{（x+2）}^{2}}$＞0，由此求得a的取值范围．
解答 解：∵函数g（x）=$\frac{a}{x+2}$在[1，2]上为减函数，∴当x∈[1，2]时，y′=$\frac{-a}{{（x+2）}^{2}}$＞0，
求得 a＞0，即a的取值范围为（0，+∞），
故选：C．
点评 本题主要考查函数的单调性的性质，利用导数研究函数的单调性，属于基础题．
练习册系列答案
相关题目
11．设双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右焦点与对称轴垂直的直线与渐近线交于A，B两点，若△OAB的面积为$\frac{\sqrt{13}bc}{3}$，则双曲线的离心率为（ ）
| A． | $\frac{\sqrt{5}}{2}$ | B． | $\frac{\sqrt{5}}{3}$ | C． | $\frac{\sqrt{13}}{2}$ | D． | $\frac{\sqrt{13}}{3}$ |
15．已知角α的终边经过点P（6，-8），点P到原点的距离为r=（ ）
| A． | 14 | B． | ±10 | C． | -10 | D． | 10 |
14．已知双曲线C：mx2-ny2=1的一个焦点为F（-5，0）．，实轴长为6，则双曲线C的渐近线方程为（ ）
| A． | y=±$\frac{4}{3}$x | B． | y=±$\frac{3}{4}$x | C． | y=±$\frac{5}{3}$x | D． | y=±$\frac{3}{5}$x |
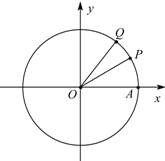如图，设A是单位圆和x轴正半轴的交点，P、Q是单位圆上的两点，O是坐标原点，∠AOP=$\frac{π}{6}$，∠AOQ=α，α∈[0，π）．