题目内容
2.已知不等式 ex≥x+1,对任意的x∈R恒成立.现有以下命题:①对?x∈R,不等式e-x>1-x恒成立;
②对?x∈(0,+∞),不等式ln(x+1)<x恒成立;
③对?x∈(0,+∞),且x≠1,不等式lnx<x-1恒成立;
④对?x∈(0,+∞),且x≠1,不等式$\frac{lnx}{x+1}+\frac{1}{x}>\frac{lnx}{x-1}$恒成立.
其中真命题的有①②③④(写出所有真命题的序号).
分析 ①由已知不等式ex≥x+1,结合对称性可得e-x>1-x恒成立;
②把已知不等式两边取对数可得不等式ln(x+1)<x恒成立;
③直接利用导数证明不等式lnx<x-1恒成立;
④对x分类证明对?x∈(0,+∞),且x≠1,不等式$\frac{lnx}{x+1}+\frac{1}{x}>\frac{lnx}{x-1}$恒成立.
解答 解:①由ex≥x+1对任意的x∈R恒成立,如图,
结合对称性可知,对?x∈R,不等式e-x>1-x恒成立,故①正确;
②由ex≥x+1,且x∈(0,+∞),
两边取对数,得x>ln(x+1),即ln(x+1)<x,故②正确;
③令f(x)=lnx-x+1,则f′(x)=$\frac{1}{x}-1$=$\frac{1-x}{x}$,
当x∈(0,1)时,f′(x)>0,当x∈(1,+∞)时,f′(x)<0,
∴f(x)max=f(1)=0,则lnx-x+1<0,即lnx<x-1,故③正确;
④当x∈(0,+∞),且x≠1时,不等式$\frac{lnx}{x+1}+\frac{1}{x}>\frac{lnx}{x-1}$等价于$\frac{2}{{x}^{2}-1}lnx-\frac{1}{x}<0$,
即$\frac{1}{x}>\frac{2}{{x}^{2}-1}lnx$,
若x∈(0,1),则$\frac{{x}^{2}-1}{2x}<lnx$,
令g(x)=$\frac{{x}^{2}-1}{2x}-lnx$,g′(x)=$\frac{4{x}^{2}-2{x}^{2}+2}{4{x}^{2}}-\frac{1}{x}=\frac{(x-1)^{2}}{4{x}^{2}}>0$,
∴g(x)在(0,1)上为增函数,则g(x)<g(1)=0,即$\frac{{x}^{2}-1}{2x}<lnx$;
若x∈(1,+∞),则$\frac{{x}^{2}-1}{2x}>lnx$,
令g(x)=$\frac{{x}^{2}-1}{2x}-lnx$,g′(x)=$\frac{4{x}^{2}-2{x}^{2}+2}{4{x}^{2}}-\frac{1}{x}=\frac{(x-1)^{2}}{4{x}^{2}}>0$,
∴g(x)在(0,1)上为增函数,则g(x)>g(1)=0,即$\frac{{x}^{2}-1}{2x}>lnx$.
∴不等式$\frac{lnx}{x+1}+\frac{1}{x}>\frac{lnx}{x-1}$恒成立.
故答案为:①②③④.
点评 本题考查命题的真假判断与应用,训练了利用导数研究函数的单调性,训练了利用导数研究函数的最值,是中档题.

| A. | 1 | B. | 2 | C. | -1 | D. | -2 |
甲电商:
| 消费金额(单位:千元) | [0,1) | [1,2) | [2,3) | [3,4) | [4,5] |
| 频数 | 50 | 200 | 350 | 300 | 100 |
| 消费金额(单位:千元) | [0,1) | [1,2) | [2,3) | [3,4) | [4,5] |
| 频数 | 250 | 300 | 150 | 100 | 200 |
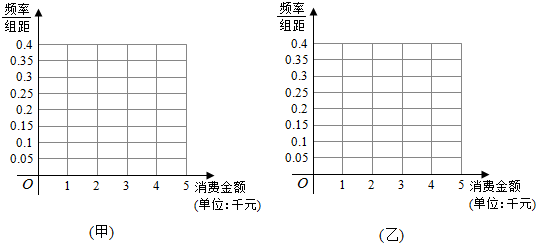
(Ⅱ)
(ⅰ)根据上述数据,估计“双十一”当天在甲电商购物的大量的消费者中,消费金额小于3千元的概率;
(ⅱ)现从“双十一”当天在甲电商购物的大量的消费者中任意调查5位,记消费金额小于3千元的人数为X,试求出X的期望和方差.
| 组号 | 超速分组 | 频数 | 频率 | 频率 组距 |
| 1 | [0,20%] | 176 | 0.88 | z |
| 2 | [20%,40%] | 12 | 0.06 | 0.0030 |
| 3 | [40%,60%] | 6 | y | 0.0015 |
| 4 | [60%,80%] | 4 | 0.02 | 0.0010 |
| 5 | [80%,100%] | x | 0.01 | 0.0005 |
(Ⅱ)若在第2,3,4,5组用分层抽样的方法随机抽取12名驾驶人员做回访调查,并在这12名驾驶人员中任意选3人,这3人中超速在[20%,80%)内的人数记为ξ,求ξ的数学期望.
(1)求函数y=f(x)的解析式;
(2)求函数y=f(x)的单调区间.
| A. | 先向右平移$\frac{π}{3}$个单位长度,再将所得点的横坐标变为原来的$\frac{1}{2}$倍,纵坐标不变 | |
| B. | 先向左平移$\frac{π}{3}$个单位长度,再将所得点的横坐标变为原来的$\frac{1}{2}$倍,纵坐标不变 | |
| C. | 先向左平移$\frac{π}{3}$个单位长度,再将所得点的横坐标变为原来的2倍,纵坐标不变 | |
| D. | 先向右平移$\frac{π}{3}$个单位长度,再将所得点的横坐标变为原来的2倍,纵坐标不变 |