题目内容
若向量
=(cosα,sinα),
=(cosβ,sinβ),则
与
一定满足( )
| a |
| b |
| a |
| b |
A、
| ||||||||
B、
| ||||||||
| C、夹角为α-β | ||||||||
D、(
|
考点:数量积判断两个平面向量的垂直关系
专题:平面向量及应用
分析:根据平面向量的数量积和坐标运算,对每一个选项进行判断即可.
解答:
解:∵向量
=(cosα,sinα),
=(cosβ,sinβ),
∴cosαsinβ-sinαcosβ=sin(β-α)=0不一定成立,∴
与
不一定平行,A错误;
•
=cosαcosβ+sinαsinβ=cos(β-α)=0不一定成立,∴
与
不一定垂直,B错误;
•
=cosαcosβ+sinαsinβ=cos(β-α),∴
与
的夹角不一定是α-β,C错误;
(
+
)•(
-
)=
2-
2=1-1=0,∴(
+
)与(
-
)一定垂直,D正确.
故选:D.
| a |
| b |
∴cosαsinβ-sinαcosβ=sin(β-α)=0不一定成立,∴
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
(
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
故选:D.
点评:本题考查了平面向量的数量积和坐标运算的应用问题,是基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
| a |
| b |
| a |
| b |
| a |
| b |
| A、充分但不必要条件 |
| B、必要但不充分条件 |
| C、充要条件 |
| D、非充非要条件 |
等差数列{an}中,已知a4、a5分别是方程x2-8x+15=0的两根,则S8=( )
| A、8 | B、16 | C、24 | D、32 |
如图所示流程图中,若a=-8,则输出结果是( )


A、2
| ||
B、-2
| ||
| C、0 | ||
| D、10 |
在下列幂函数中,是偶函数且在(0,+∞)上是增函数的是( )
| A、y=x-2 | ||
B、y=x
| ||
C、y=x
| ||
D、y=x
|
已知sinα=2cosα,则
的值为( )
| sinα+cosα |
| sinα-cosα |
| A、3 | B、-3 | C、2 | D、-2 |
设i为虚数单位,复数 z1=3-ai,z2=1+2i,若
是纯虚数,则实数a的值为( )
| z1 |
| z2 |
A、-
| ||
B、
| ||
| C、-6 | ||
| D、6 |
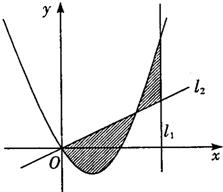 已知二次函数f(x)=3x2-3x,直线l1:x=2和l2:y=3tx(其中t为常数,且0<t<1),直线l2与函数f(x)的图象以及直线l1、l2与函数f(x)的图象所围成的封闭图形如图中阴影所示,设这两个阴影区域的面积之和为S(t).
已知二次函数f(x)=3x2-3x,直线l1:x=2和l2:y=3tx(其中t为常数,且0<t<1),直线l2与函数f(x)的图象以及直线l1、l2与函数f(x)的图象所围成的封闭图形如图中阴影所示,设这两个阴影区域的面积之和为S(t).