题目内容
抛物线y=-3x2-x+4与坐标轴的交点个数是 .
考点:二次函数的性质
专题:函数的性质及应用
分析:令抛物线解析式中x=0,求出对应的y的值,即为抛物线与y轴交点的纵坐标,确定出抛物线与y轴的交点坐标,令抛物线解析式中y=0,得到关于x的一元二次方程,求出方程的解有两个,可得出抛物线与x轴有两个交点,综上,得到抛物线与坐标轴的交点个数.
解答:
解:抛物线解析式y=-3x2-x+4,
令x=0,解得:y=4,
∴抛物线与y轴的交点为(0,4),
令y=0,得到-3x2-x+4=0,即3x2+x-4=0,
分解因式得:(3x+4)(x-1)=0,
解得:x1=-
,x2=1,
∴抛物线与x轴的交点分别为(-
,0),(1,0),
综上,抛物线与坐标轴的交点个数为3.
故答案为:3
令x=0,解得:y=4,
∴抛物线与y轴的交点为(0,4),
令y=0,得到-3x2-x+4=0,即3x2+x-4=0,
分解因式得:(3x+4)(x-1)=0,
解得:x1=-
| 4 |
| 3 |
∴抛物线与x轴的交点分别为(-
| 4 |
| 3 |
综上,抛物线与坐标轴的交点个数为3.
故答案为:3
点评:此题考查了抛物线与x轴的交点,以及一元二次方程的解法,其中令抛物线解析式中x=0,求出的y值即为抛物线与y轴交点的纵坐标;令y=0,求出对应的x的值,即为抛物线与x轴交点的横坐标.

练习册系列答案
 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
已知双曲线
-
=1(b>0)的左顶点为A1,右顶点A2,右焦点为F,点P为双曲线上一点,
•
=0,
•
=
,则双曲线的离心率为( )
| x2 |
| 3 |
| y2 |
| b2 |
| PF |
| A1A2 |
| PA1 |
| PA2 |
| 10 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若函数y=x2+bx+3在(-∞,1]上是单调递减函数,则有( )
| A、b≥2 | B、b≤2 |
| C、b≥-2 | D、b≤-2 |
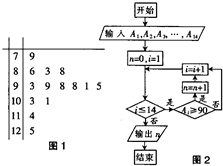 如图1是某高三学生14次数学考试成绩的茎叶图,现将该14个数据依次记为A1,A2,…A14,并输入如图2所示的一个算法流程图,那么该算法流程图运行结束时输出的n值是( )
如图1是某高三学生14次数学考试成绩的茎叶图,现将该14个数据依次记为A1,A2,…A14,并输入如图2所示的一个算法流程图,那么该算法流程图运行结束时输出的n值是( )