题目内容
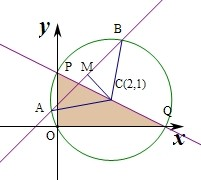
已知平面区域
被圆C及其内部所覆盖.
(1)当圆C的面积最小时,求圆C的方程;
(2)若斜率为1的直线l与(1)中的圆C交于不同的两点A、B,且满足S△ABC=
,求直线l的方程.
|
(1)当圆C的面积最小时,求圆C的方程;
(2)若斜率为1的直线l与(1)中的圆C交于不同的两点A、B,且满足S△ABC=
| 5 |
| 2 |
考点:简单线性规划,直线的一般式方程,圆的标准方程,直线与圆的位置关系
专题:直线与圆
分析:(1)作出平面区域,利用圆C的面积最小时,确定圆心和圆的半径即可求圆C的方程;
(2)设出直线l的方程,利用直线和圆的位置关系结合S△ABC=
,建立方程关系,即可求直线l的方程.
(2)设出直线l的方程,利用直线和圆的位置关系结合S△ABC=
| 5 |
| 2 |
解答:
解:(1)作出不等式组对应的平面区域,由O(0,0),P(4,0),Q(0,2)构成的三角形及其内部,且△OPQ是直角三角形,
由于覆盖它的且面积最小的圆是其外接圆,
∴圆心是Rt△OPQ的斜边PQ的中点C(2,1),半径r=|OC|=
=
,
∴圆C的方程是(x-2)2+(y-1)2=5.
(2)∵圆C的方程是(x-2)2+(y-1)2=5.
∴设直线l的方程为y=x+b,
则圆心C到直线AB的距离d=
=
,
将直线方程代入圆的方程得
∵BC=
,
∴AB=2
=2
=2
,
∵S△ABC=
,
∴S△ABC=
=
•AB•d,
即
×
×2
=
,
即
•
=
,
∴|b+1|•
=5,
即(b+1)2•[10-(b+1)2]=25,
∴(b+1)4-10(b+1)2+25=0,
即[(b+1)2-5]2=0,
∴(b+1)2=5,
解得b=-1±
,满足条件,
∴直线l的方程的方程为y=x+(-1±
).
由于覆盖它的且面积最小的圆是其外接圆,
∴圆心是Rt△OPQ的斜边PQ的中点C(2,1),半径r=|OC|=
| 22+12 |
| 5 |
∴圆C的方程是(x-2)2+(y-1)2=5.
(2)∵圆C的方程是(x-2)2+(y-1)2=5.
∴设直线l的方程为y=x+b,
则圆心C到直线AB的距离d=
| |2-1+b| | ||
|
| |b+1| | ||
|
将直线方程代入圆的方程得
∵BC=
| 5 |

∴AB=2
| BC2-d2 |
5-(
|
5-
|
∵S△ABC=
| 5 |
| 2 |
∴S△ABC=
| 5 |
| 2 |
| 1 |
| 2 |
即
| 1 |
| 2 |
| |b+1| | ||
|
5-
|
| 5 |
| 2 |
即
| |b+1| | ||
|
|
| 5 |
| 2 |
∴|b+1|•
| 10-(b+1)2 |
即(b+1)2•[10-(b+1)2]=25,
∴(b+1)4-10(b+1)2+25=0,
即[(b+1)2-5]2=0,
∴(b+1)2=5,
解得b=-1±
| 5 |
∴直线l的方程的方程为y=x+(-1±
| 5 |
点评:本题主要考查线性规划的应用,以及圆的方程的求法,利用直线和圆的位置关系求出相交线AB的长度,结合三角形的面积公式是解决本题的关键,运算量较大,综合性较强.考查学生的运算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设函数f(x)=ex-x-2,用二分法求方程ex-x-2=0在区间(-1,3)内的近似解的过程中得到f(-1)<0,f(0)<0,f(1)<0,f(2)>0,f(3)>0,则方程至少有一个根落在( )
| A、(-1,0) |
| B、(0,1) |
| C、(1,2) |
| D、(2,3) |
直线kx-y=k+2和x-ky=k(k>1)与y轴围成的三角形的面积的最小值为( )
| A、3 | ||||
B、
| ||||
C、
| ||||
D、
|
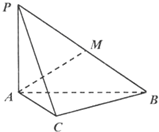 如图,三棱锥P-ABC中,∠ACB=90°,PA⊥底面ABC.
如图,三棱锥P-ABC中,∠ACB=90°,PA⊥底面ABC.