��Ŀ����
11��������D�ϵĺ���f��x���������㣺������x��D�����ڳ���M��0������|f��x��|��M���������f��x����D�ϵ��н纯��������M��Ϊ����f��x�����Ͻ磺��1����f��x��=$\frac{x}{x+1}$���ж�f��x����[-$\frac{1}{2}$��$\frac{1}{2}$]���Ƿ��н纯�������ǣ���˵�����ɣ���д��f��x���������Ͻ��ֵ�ļ��ϣ������ǣ�Ҳ��˵�����ɣ�
��2��������g��x��=1+a•��$\frac{1}{2}$��x+��$\frac{1}{4}$��x��[0��+�ޣ�������3Ϊ�Ͻ���н纯������ʵ��a��ȡֵ��Χ��
���� ��1������ɵ�f��x����[-$\frac{1}{2}$��$\frac{1}{2}$]�������������Ӷ��ɵ�|f��x��|��1���Ӷ���ã�
��2��������֪-3��1+a•��$\frac{1}{2}$��x+��$\frac{1}{4}$��x��3��[0��+�ޣ��Ϻ�������Ӷ��ɵ�-��4•2x+2-x����a��2•2x-2-x��[0��+�ޣ��Ϻ�������Ӷ���ã�
��� �⣺��1��f��x��=$\frac{x}{x+1}$=1-$\frac{1}{x+1}$��
��f��x����[-$\frac{1}{2}$��$\frac{1}{2}$]������������
��f��-$\frac{1}{2}$����f��x����f��$\frac{1}{2}$����
��-1��f��x����$\frac{1}{3}$��
��|f��x��|��1��
��f��x�����н纯����
��f��x���������Ͻ��ֵ�ļ�����[1��+�ޣ���
��2����g��x��=1+a•��$\frac{1}{2}$��x+��$\frac{1}{4}$��x��[0��+�ޣ�������3Ϊ�Ͻ���н纯����
��-3��1+a•��$\frac{1}{2}$��x+��$\frac{1}{4}$��x��3��[0��+�ޣ��Ϻ������
��-��4•2x+2-x����a��2•2x-2-x��[0��+�ޣ��Ϻ������
��-��4•2x+2-x����[0��+�ޣ��ϵ����ֵΪ-5��
2•2x-2-x��[0��+�ޣ��ϵ���СֵΪ1��
��-5��a��1��
��ʵ��a��ȡֵ��ΧΪ[-5��1]��
���� ���⿼���˺����ĵ����Ե��ж���Ӧ�ã�ͬʱ������ѧ����ѧϰ������ת��˼���Ӧ�ã������е��⣮

| A�� | ����ƽ��$\frac{��}{12}$����λ | B�� | ����ƽ��$\frac{��}{12}$����λ | ||
| C�� | ����ƽ��$\frac{��}{6}$����λ | D�� | ����ƽ��$\frac{��}{6}$����λ |
| A�� | a��8 | B�� | a��8 | C�� | a��4 | D�� | a��4 |
| A�� | 2�� | B�� | �� | C�� | $\frac{��}{2}$ | D�� | $\frac{��}{4}$ |
| A�� | ��x+$\frac{3}{5}$��2+��y-$\frac{9}{5}$��2=$\frac{19}{5}$ | B�� | ��x-$\frac{3}{5}$��2+��y-$\frac{9}{5}$��2=$\frac{19}{5}$ | C�� | ��x-$\frac{3}{5}$��2+��y+$\frac{9}{5}$��2=$\frac{19}{5}$ | D�� | ���϶����� |
| A�� | 5 | B�� | 4 | C�� | 3 | D�� | 1 |
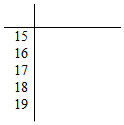 Ϊ�˵���ij�������Ե�����������о������ڸõ��������ȡ��30λ��ͬ�����Ծ���������߲������ֽ������������£���λ��cm����
Ϊ�˵���ij�������Ե�����������о������ڸõ��������ȡ��30λ��ͬ�����Ծ���������߲������ֽ������������£���λ��cm����