题目内容
:如图,在三棱锥 中,
中,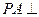 底面ABC,
底面ABC,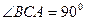 ,AP="AC," 点
,AP="AC," 点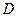 ,
, 分别在棱
分别在棱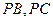 上,且BC//平面ADE
上,且BC//平面ADE
(Ⅰ)求证:DE⊥平面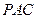 ;
;
 (Ⅱ)当二面角
(Ⅱ)当二面角 为直二面角时,求多面体ABCED与PAED的体积比。
为直二面角时,求多面体ABCED与PAED的体积比。
 中,
中,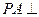 底面ABC,
底面ABC,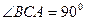 ,AP="AC," 点
,AP="AC," 点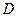 ,
, 分别在棱
分别在棱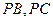 上,且BC//平面ADE
上,且BC//平面ADE(Ⅰ)求证:DE⊥平面
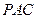 ;
; (Ⅱ)当二面角
(Ⅱ)当二面角 为直二面角时,求多面体ABCED与PAED的体积比。
为直二面角时,求多面体ABCED与PAED的体积比。:略
:(Ⅰ) BC//平面ADE, BC
BC//平面ADE, BC 平面PBC, 平面PBC
平面PBC, 平面PBC 平面ADE=DE
平面ADE=DE
 BC//ED …………2分
BC//ED …………2分
∵PA⊥底面ABC,BC 底面ABC ∴PA⊥BC. ………3分
底面ABC ∴PA⊥BC. ………3分
又 ,∴AC⊥BC.
,∴AC⊥BC.
∵PA AC="A," ∴BC⊥平面PAC. …………5分
AC="A," ∴BC⊥平面PAC. …………5分
∴DE⊥平面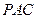 . …………6分
. …………6分
(Ⅱ)由(Ⅰ)知, DE⊥平面PAC,
又∵AE 平面PAC,PE
平面PAC,PE 平面PAC,∴DE⊥AE,DE⊥PE,
平面PAC,∴DE⊥AE,DE⊥PE,
∴∠AEP为二面角 的平面角, …………8分
的平面角, …………8分
∴ ,即AE⊥PC, …………9分
,即AE⊥PC, …………9分
∵AP="AC," ∴E是PC的中点,ED是 PBC的中位线。………10分
PBC的中位线。………10分
 ………12分
………12分
 BC//平面ADE, BC
BC//平面ADE, BC 平面PBC, 平面PBC
平面PBC, 平面PBC 平面ADE=DE
平面ADE=DE BC//ED …………2分
BC//ED …………2分∵PA⊥底面ABC,BC
 底面ABC ∴PA⊥BC. ………3分
底面ABC ∴PA⊥BC. ………3分又
 ,∴AC⊥BC.
,∴AC⊥BC. ∵PA
 AC="A," ∴BC⊥平面PAC. …………5分
AC="A," ∴BC⊥平面PAC. …………5分∴DE⊥平面
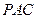 . …………6分
. …………6分(Ⅱ)由(Ⅰ)知, DE⊥平面PAC,
又∵AE
 平面PAC,PE
平面PAC,PE 平面PAC,∴DE⊥AE,DE⊥PE,
平面PAC,∴DE⊥AE,DE⊥PE,∴∠AEP为二面角
 的平面角, …………8分
的平面角, …………8分∴
 ,即AE⊥PC, …………9分
,即AE⊥PC, …………9分∵AP="AC," ∴E是PC的中点,ED是
 PBC的中位线。………10分
PBC的中位线。………10分 ………12分
………12分
练习册系列答案
相关题目
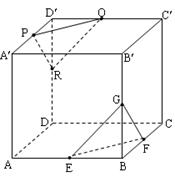
 与
与 互相平行的一个充分条件是
互相平行的一个充分条件是 都平行于同一平面
都平行于同一平面 中,点E,D分别是
中,点E,D分别是 与BC的中点.
与BC的中点. EB//平面AD
EB//平面AD .
.
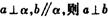

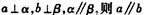
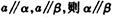
 为两个平
为两个平 面,则下列四个命题中,正确的命题是( )
面,则下列四个命题中,正确的命题是( ) 且
且 ,则
,则
 ,则
,则
 ,则
,则
 是两条异面直线,且
是两条异面直线,且 ,则
,则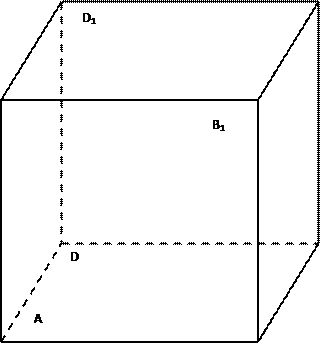
 同时垂直直线c,那么直线a与b的关系是( )
同时垂直直线c,那么直线a与b的关系是( )