题目内容
8.已知中心在原点O的椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)其短轴长为2$\sqrt{2}$,一焦点F(c,0)(c>0),且2a2=3c2,过点A(3,0)的直线与椭圆相交于P,Q两点.(Ⅰ)若$\overrightarrow{OP}$•$\overrightarrow{OQ}$=0,求直线PQ的方程;
(Ⅱ)设$\overrightarrow{AP}$=λ$\overrightarrow{AQ}$(λ>1).点M为P关于x轴的对称点,证明:$\overrightarrow{FM}$=-λ$\overrightarrow{FQ}$.
分析 (I)由题意可得:$\left\{\begin{array}{l}{2b=2\sqrt{2}}\\{2{a}^{2}=3{c}^{2}}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,可得椭圆的标准方程为:$\frac{{x}^{2}}{6}+\frac{{y}^{2}}{2}=1$.设直线PQ的方程为:my=x-3,Q(x1,y1),P(x2,y2).与椭圆方程联立可得:(m2+3)y2+6my+3=0.由$\overrightarrow{OP}$•$\overrightarrow{OQ}$=0,可得x1x2+y1y2=0,即(my1+3)(my2+3)+y1y2=0,把根与系数的关系代入可得m.
(II)F(2,0).由(I)可得:M(x2,-y2),由于$\overrightarrow{AP}$=λ$\overrightarrow{AQ}$(λ>1).可得y2=λy1.即可证明.
解答  解:(I)由题意可得:$\left\{\begin{array}{l}{2b=2\sqrt{2}}\\{2{a}^{2}=3{c}^{2}}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,解得b=$\sqrt{2}$,c=2,a2=6.
解:(I)由题意可得:$\left\{\begin{array}{l}{2b=2\sqrt{2}}\\{2{a}^{2}=3{c}^{2}}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,解得b=$\sqrt{2}$,c=2,a2=6.
∴椭圆的标准方程为:$\frac{{x}^{2}}{6}+\frac{{y}^{2}}{2}=1$.
设直线PQ的方程为:my=x-3,Q(x1,y1),P(x2,y2).
联立$\left\{\begin{array}{l}{my=x-3}\\{{x}^{2}+3{y}^{2}=6}\end{array}\right.$,化为:(m2+3)y2+6my+3=0,
∴y1+y2=-$\frac{6m}{{m}^{2}+3}$,y1y2=$\frac{3}{{m}^{2}+3}$.
∵$\overrightarrow{OP}$•$\overrightarrow{OQ}$=0,
∴x1x2+y1y2=0,
∴(my1+3)(my2+3)+y1y2=0,
化为(m2+1)y1y2+3m(y1+y2)+9=0,
∴$\frac{3({m}^{2}+1)}{{m}^{2}+3}$-$\frac{18{m}^{2}}{{m}^{2}+3}$+9=0,
化为:m2=5,
解得m=$±\sqrt{5}$,
∴直线PQ的方程为:x$±\sqrt{5}$y-3=0.
(II)F(2,0).
由(I)可得:M(x2,-y2),
∵$\overrightarrow{AP}$=λ$\overrightarrow{AQ}$(λ>1).
∴y2=λy1.
∴-y2=-λy1,
∴$\overrightarrow{FM}$=-λ$\overrightarrow{FQ}$.
点评 本题考查了直线与椭圆相交问题、一元二次方程的根与系数的关系、向量垂直与数量积的关系、直线方程、向量共线定理,考查了推理能力与计算能力,属于难题.

 寒假学与练系列答案
寒假学与练系列答案 在等腰梯形ABCD中(如图),AB∥CD,DE⊥AB,AB=5,CD=3,∠DAB=$\frac{π}{3}$,现沿DE将等腰梯形折成直二面角.
在等腰梯形ABCD中(如图),AB∥CD,DE⊥AB,AB=5,CD=3,∠DAB=$\frac{π}{3}$,现沿DE将等腰梯形折成直二面角.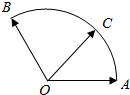 如图,给定单位向量$\overrightarrow{OA}$和$\overrightarrow{OB}$,它们的夹角为120°,点C在以O为圆心的$\widehat{AB}$上运动.若$\overrightarrow{OC}=x\overrightarrow{OA}+y\overrightarrow{OB}$,其中x,y∈R,则x+2y的最大值是$\frac{2\sqrt{21}}{3}$.
如图,给定单位向量$\overrightarrow{OA}$和$\overrightarrow{OB}$,它们的夹角为120°,点C在以O为圆心的$\widehat{AB}$上运动.若$\overrightarrow{OC}=x\overrightarrow{OA}+y\overrightarrow{OB}$,其中x,y∈R,则x+2y的最大值是$\frac{2\sqrt{21}}{3}$.