题目内容
3.若直线y=x+$\sqrt{6}$与椭圆x2+$\frac{{y}^{2}}{{m}^{2}}$=1(m>0且m≠1)只有一个公共点,则该椭圆的长轴长为2$\sqrt{5}$.分析 直线方程与椭圆方程联立:(m2+1)x2+2$\sqrt{6}$x+6-m2=0,根据直线y=x+$\sqrt{6}$与椭圆x2+$\frac{{y}^{2}}{{m}^{2}}$=1(m>0且m≠1)只有一个公共点,可得△=0,解出即可得出.
解答 解:联立$\left\{\begin{array}{l}{y=x+\sqrt{6}}\\{{x}^{2}+\frac{{y}^{2}}{{m}^{2}}=1}\end{array}\right.$,化为:(m2+1)x2+2$\sqrt{6}$x+6-m2=0,
∵直线y=x+$\sqrt{6}$与椭圆x2+$\frac{{y}^{2}}{{m}^{2}}$=1(m>0且m≠1)只有一个公共点,
∴△=24-4(m2+1)(6-m2)=0,
化为:m4-5m2=0,m>0且m≠1,
解得m=$\sqrt{5}$.
∴该椭圆的长轴长为2$\sqrt{5}$.
故答案为:2$\sqrt{5}$.
点评 本题考查了直线与椭圆相切与判别式的关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
13.已知实数x、y、z满足x2+y2+z2=4,则(2x-y)2+(2y-z)2+(2z-x)2的最大值是( )
| A. | 12 | B. | 20 | C. | 28 | D. | 36 |
14.关于x的不等式$\frac{2x-3a}{x+2a}≤1(a<0)$的解集是( )
| A. | [5a,-2a) | B. | (-∞,5a]∪(-2a,+∞) | C. | (-2a,5a]? | D. | (-∞,5a] |
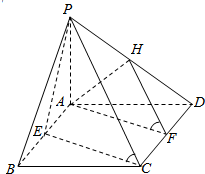 如图所示,四棱锥P-ABCD的底面ABCD为矩形,PA⊥平面ABCD,PA=AD=2CD=2,E,F,H分别为AB,CD,PD的中点,求证:(1)平面AFH∥平面PCE;(2)求VD-AHF.
如图所示,四棱锥P-ABCD的底面ABCD为矩形,PA⊥平面ABCD,PA=AD=2CD=2,E,F,H分别为AB,CD,PD的中点,求证:(1)平面AFH∥平面PCE;(2)求VD-AHF.