题目内容
10.已知O为坐标原点,F是椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点,A,B分别为C的左,右顶点.P为C上一点,且PF⊥x轴.过点A的直线l与线段PF交于点M,与y轴交于点E.若直线BM经过OE的中点,则C的离心率为$\frac{1}{3}$.分析 由题意可得F,A,B的坐标,设出直线AE的方程为y=k(x+a),分别令x=-c,x=0,可得M,E的坐标,再由中点坐标公式可得H的坐标,运用三点共线的条件:斜率相等,结合离心率公式,即可得到所求值.
解答 解:由题意可设F(-c,0),A(-a,0),B(a,0),
令x=-c,代入椭圆方程可得y=±$\frac{{b}^{2}}{a}$,可得P(-c,±$\frac{{b}^{2}}{a}$).
设直线AE的方程为y=k(x+a),
令x=-c,可得M(-c,k(a-c)),令x=0,可得E(0,ka),
设OE的中点为H,可得H(0,$\frac{ka}{2}$),
由B,H,M三点共线,可得kBH=kBM,即$\frac{a-c}{a+c}$=$\frac{1}{2}$,即为a=3c,
可得e=$\frac{c}{a}$=$\frac{1}{3}$,
故答案为:$\frac{1}{3}$.
点评 本题考查椭圆的离心率的求法,注意运用椭圆的方程和性质,以及直线方程的运用和三点共线的条件:斜率相等,考查化简整理的运算能力,属于中档题.

练习册系列答案
相关题目
10.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=1,|$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{3}$,$\overrightarrow{a}$•($\overrightarrow{a}$-$\overrightarrow{b}$)=0,则|$\overrightarrow{b}$-2$\overrightarrow{a}$|=( )
| A. | 2 | B. | 2$\sqrt{3}$ | C. | 4 | D. | 4$\sqrt{3}$ |
11.“中国式过马路”是网友对部分中国人集体闯红灯现象的一种调侃,即“凑够一撮人就可以走了,和红绿灯无关”,某校研究性学习小组对全校学生按“跟从别人闯红灯”,“从不闯红灯”、“带头闯红灯”等三种形式进行调查,获得下表数据:
用分层抽样的方法从所有被调查的人中抽取一个容量为n的样本,其中在“跟从别人闯红灯”的人中抽取了66人.
(Ⅰ)求n的值;
(Ⅱ)在所抽取的“带头闯红灯”的人中,在选取2人参加星期天社区组织的“文明交通”宣传活动,求这2人中至少有一人是女生的概率.
| 跟从别人闯红灯 | 从不闯红灯 | 带头闯红灯 | |
| 男生 | 980 | 410 | 60 |
| 女生 | 340 | 150 | 60 |
(Ⅰ)求n的值;
(Ⅱ)在所抽取的“带头闯红灯”的人中,在选取2人参加星期天社区组织的“文明交通”宣传活动,求这2人中至少有一人是女生的概率.
8.已知f(x)=$\left\{\begin{array}{l}{-2,0<x<1}\\{1,x≥1}\end{array}$在区间(0,4)内任取一个为x,则不等式log2x-(log${\;}_{\frac{1}{4}}$4x-1)f(log3x+1)≤$\frac{7}{2}$的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{5}{12}$ | C. | $\frac{1}{2}$ | D. | $\frac{7}{12}$ |
20.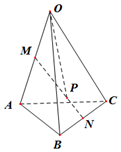 已知M、N分别是四面体OABC的棱OA,BC的中点,点P在线MN上,且MP=2PN,设向量$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,则$\overrightarrow{OP}$=( )
已知M、N分别是四面体OABC的棱OA,BC的中点,点P在线MN上,且MP=2PN,设向量$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,则$\overrightarrow{OP}$=( )
 已知M、N分别是四面体OABC的棱OA,BC的中点,点P在线MN上,且MP=2PN,设向量$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,则$\overrightarrow{OP}$=( )
已知M、N分别是四面体OABC的棱OA,BC的中点,点P在线MN上,且MP=2PN,设向量$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,则$\overrightarrow{OP}$=( )| A. | $\frac{1}{6}$$\overrightarrow{a}$+$\frac{1}{6}$$\overrightarrow{b}$+$\frac{1}{6}$$\overrightarrow{c}$ | B. | $\frac{1}{3}$$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$+$\frac{1}{3}$$\overrightarrow{c}$ | C. | $\frac{1}{6}$$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$+$\frac{1}{3}$$\overrightarrow{c}$ | D. | $\frac{1}{3}$$\overrightarrow{a}$+$\frac{1}{6}$$\overrightarrow{b}$+$\frac{1}{6}$$\overrightarrow{c}$ |