题目内容
log2log3log4x=log3log4log2y=log4log2log3z=0,则x+y+z=
- A.50
- B.58
- C.89
- D.111
C
分析:根据对数的性质逐一进行运算,可得x、y、z的值,即可得到答案.
解答:∵log2log3log4x=0
∴log3log4x=1
∴log4x=3
∴x=64
∵log3log4log2y=0
∴log4log2y=1
∴log2y=4
∴y=16
∵log4log2log3z=0
∴log2log3z=1
∴log3z=2
∴z=9
∴x+y+z=64+16+9=89
故选C
点评:对数的运算性质里:1的对数等于0,底数的对数等于1,比较常用,要求熟记.
分析:根据对数的性质逐一进行运算,可得x、y、z的值,即可得到答案.
解答:∵log2log3log4x=0
∴log3log4x=1
∴log4x=3
∴x=64
∵log3log4log2y=0
∴log4log2y=1
∴log2y=4
∴y=16
∵log4log2log3z=0
∴log2log3z=1
∴log3z=2
∴z=9
∴x+y+z=64+16+9=89
故选C
点评:对数的运算性质里:1的对数等于0,底数的对数等于1,比较常用,要求熟记.

练习册系列答案
相关题目
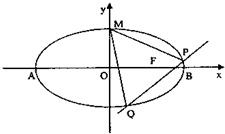 已知椭圆
已知椭圆