题目内容

直线l：y=k（x+2
2
）与圆x2+y2=4相交于A、B两点，O为坐标原点，△ABO的面积为S，求函数S=f（k）的表达式．
分析：原点到直线l的距离d=
2
2
|k|
1+k2
，弦长|AB|=2
|OA|2-d2
=2
4-
8k2
1+k2
，由此能够求出，△ABO的面积为S，进而得到函数S=f（k）的表达式．
解答：解：原点到直线l的距离d=
2
2
|k|
1+k2
，
弦长|AB|=2
|OA|2-d2
=2
4-
8k2
1+k2
，
所以S=
1
2
×2
4-
8k2
1+k2
×
2
2
|k|
1+k2
=
4
2
•
k2(1-k2)
1+k2
，
即f（k）=
4
2
•
k2(1-k2)
1+k2
（-1＜k＜1，且k≠0）．
点评：本题考查直线和圆的位置关系和应用，解题时要认真审题，仔细解答，避免不必要的错误．
练习册系列答案
相关题目
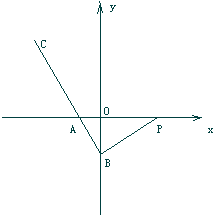如图，已知直角三角形PAB的直角顶点为B，点P的坐标为（3，0），点B在y轴上，点A在x轴的负半轴上，在BA的延长线上取一点C，使
BC
=3
BA
．
（1）当B在y轴上移动时，求动点C的轨迹方程；
（2）若直线l：y=k（x-1）与点C的轨迹交于M、N两点，设D（-1，0），当∠MDN为锐角时，求的取值范围．
直线l：y=k（x-2）+2与圆x2+y2-2x-2y=0有两个不同的公共点，则k的取值范围是（　　）
（2008•成都三模）已知O为坐标原点，点E、F的坐标分别为（-
2
，0）、（
2
，0），点A、N满足
AE
=2
3
，
ON
=
1
2
(
OA
+
OF
)，过点N且垂直于AF的直线交线段AE于点M，设点M的轨迹为C．
（1）求轨迹C的方程；
（2）若轨迹C上存在两点P和Q关于直线l：y=k（x+1）（k≠0）对称，求k的取值范围；
（3）在（2）的条件下，设直线l与轨迹C交于不同的两点R、S，对点B（1，0）和向量a=（-
3
，3k），求
BR
•
BS
-|a|2取最大值时直线l的方程．
已知圆C：（x+1）2+（y-2）2=4
（1）若直线l：y=k（x-2）与圆C有且只有一个公共点，求直线l的斜率k的值；
（2）若直线m：y=kx+2被圆C截得的弦AB满足OA⊥OB（O是坐标原点），求直线m的方程．
已知抛物线C：y2=8x，O为坐标原点，动直线l：y=k（x+2）与抛物线C交于不同两点A，B
（1）求证：
OA
•
OB
为常数；
（2）求满足
OM
=
OA
+
OB
的点M的轨迹方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网