题目内容
对于区间[a,b](或(a,b)、[a,b)、(a,b]),我们定义|b-a|为该区间的长度,特别地,[a,+∞)和(-∞,b]的区间长度为正无穷大.
(1)关于x的不等式ax2+(2a-1)x-2≤0的解集的区间长度不小于4,求实数a的取值范围;
(2)关于x的不等式(x2-2x-24)[x2-(2m+6)x+(m2+6m)]<0恰好有3个整数解,求实数m的取值范围.
(1)关于x的不等式ax2+(2a-1)x-2≤0的解集的区间长度不小于4,求实数a的取值范围;
(2)关于x的不等式(x2-2x-24)[x2-(2m+6)x+(m2+6m)]<0恰好有3个整数解,求实数m的取值范围.
考点:一元二次不等式的应用
专题:计算题,不等式的解法及应用
分析:(1)分类讨论,利用关于x的不等式ax2+(2a-1)x-2≤0的解集的区间长度不小于4,即可求实数a的取值范围;
(2)不等式(x2-2x-24)[x2-(2m+6)x+(m2+6m)]<0为(x-6)(x+4)(x-m)(x-m-6)<0,根据关于x的不等式(x2-2x-24)[x2-(2m+6)x+(m2+6m)]<0恰好有3个整数解,即可求实数m的取值范围.
(2)不等式(x2-2x-24)[x2-(2m+6)x+(m2+6m)]<0为(x-6)(x+4)(x-m)(x-m-6)<0,根据关于x的不等式(x2-2x-24)[x2-(2m+6)x+(m2+6m)]<0恰好有3个整数解,即可求实数m的取值范围.
解答:
解:(1)a=0时,解集为[-2,+∞)符合要求;
a>0时,解集为[-2,
],则需
-(-2)≥4,∴0<a≤
;
a<0时,令
=-2,∴a=-
,
∴实数a的取值范围是(-∞,
];
(2)不等式(x2-2x-24)[x2-(2m+6)x+(m2+6m)]<0为(x-6)(x+4)(x-m)(x-m-6)<0,
∵关于x的不等式(x2-2x-24)[x2-(2m+6)x+(m2+6m)]<0恰好有3个整数解,
∴m=-4或m=0,或-3<m<-2,或-2<m<-1.
a>0时,解集为[-2,
| 1 |
| a |
| 1 |
| a |
| 1 |
| 2 |
a<0时,令
| 1 |
| a |
| 1 |
| 2 |
∴实数a的取值范围是(-∞,
| 1 |
| 2 |
(2)不等式(x2-2x-24)[x2-(2m+6)x+(m2+6m)]<0为(x-6)(x+4)(x-m)(x-m-6)<0,
∵关于x的不等式(x2-2x-24)[x2-(2m+6)x+(m2+6m)]<0恰好有3个整数解,
∴m=-4或m=0,或-3<m<-2,或-2<m<-1.
点评:熟练掌握一元二次不等式的解法及其新定义是解题的关键.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
等差数列{an}中,若a3=5,a5=3,则a1+a7=( )
| A、4 | B、8 | C、-4 | D、-8 |
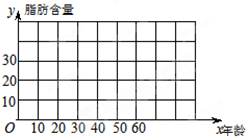 在关于人体脂肪含量y(百分比)和年龄x关系的研究中,得到如下一组数据
在关于人体脂肪含量y(百分比)和年龄x关系的研究中,得到如下一组数据
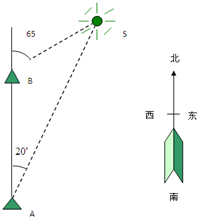 如图,一艘船以32.2n mile/h的速度向正北航行.在A处看灯塔S在船的北偏东20°的方向,30min后航行到B处,在B处看灯塔在船的北偏东65°的方向,已知距离此灯塔6.5n mile以外的海区为航行安全区域,这艘船可以继续沿正北方向航行吗?
如图,一艘船以32.2n mile/h的速度向正北航行.在A处看灯塔S在船的北偏东20°的方向,30min后航行到B处,在B处看灯塔在船的北偏东65°的方向,已知距离此灯塔6.5n mile以外的海区为航行安全区域,这艘船可以继续沿正北方向航行吗?