题目内容
已知函数f(x)=
,a∈R.
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若f(x)在(1,2)上是单调函数,求a的取值范围.
| x2 |
| x-a |
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若f(x)在(1,2)上是单调函数,求a的取值范围.
考点:函数的单调性及单调区间
专题:函数的性质及应用,导数的综合应用
分析:本题考察函数的单调性.
(Ⅰ)先写出函数的定义域,然后求导数,分a=0,a>0,a<0,利用导数的符号讨论函数的单调性即可,
(Ⅱ)结合(Ⅰ)中的函数单调性,对a进行分类讨论,又x∈(1,2),分成a≤0,0<2a≤1,1<2a<2,2a≥2四种情况进行讨论.
(Ⅰ)先写出函数的定义域,然后求导数,分a=0,a>0,a<0,利用导数的符号讨论函数的单调性即可,
(Ⅱ)结合(Ⅰ)中的函数单调性,对a进行分类讨论,又x∈(1,2),分成a≤0,0<2a≤1,1<2a<2,2a≥2四种情况进行讨论.
解答:
解:(Ⅰ)f(x)的定义域为{x|x≠a}.f′(x)=
.
①当a=0时,f(x)=x(x≠0),f'(x)=1,则x∈(-∞,0),(0,+∞)时,f(x)为增函数;
②当a>0时,
由f'(x)>0得,x>2a或x<0,由于此时0<a<2a,所以x>2a时,f(x)为增函数,x<0时,f(x)为增函数;
由f'(x)<0得,0<x<2a,考虑定义域,当0<x<a,f(x)为减函数,a<x<2a时,f(x)为减函数;
③当a<0时,
由f'(x)>0得,x>0或x<2a,由于此时2a<a<0,所以当x<2a时,f(x)为增函数,x>0时,f(x)为增函数.
由f'(x)<0得,2a<x<0,考虑定义域,当2a<x<a,f(x)为减函数,a<x<0时,f(x)为减函数.
综上,当a=0时,函数f(x)的单调增区间为(-∞,0),(0,+∞).
当a>0时,函数f(x)的单调增区间为x∈(-∞,0),(2a,+∞),单调减区间为(0,a),(a,2a).
当a<0时,函数f(x)的单调增区间为x∈(-∞,2a),(0,+∞),单调减区间为(2a,a),(a,0).
(Ⅱ)①当a≤0时,由(Ⅰ) 可得,f(x)在(1,2)单调增,且x∈(1,2)时,x≠a.
②当0<2a≤1时,即0<a≤
时,由(Ⅰ) 可得,f(x)在(2a,+∞)单调增,即在(1,2)单调增,且x∈(1,2)时,x≠a.
③当1<2a<2时,即
<a<1时,由(Ⅰ) 可得,f(x)在(1,2)上不具有单调性,不合题意.
④当2a≥2,即a≥1时,由(Ⅰ)可得,f(x)在(0,a),(a,2a)为减函数,
同时需注意a∉(1,2),满足这样的条件时f(x)在(1,2)单调减,所以此时a=1或a≥2.
综上所述,a≤
或a=1或a≥2.
| x(x-2a) |
| (x-a)2 |
①当a=0时,f(x)=x(x≠0),f'(x)=1,则x∈(-∞,0),(0,+∞)时,f(x)为增函数;
②当a>0时,
由f'(x)>0得,x>2a或x<0,由于此时0<a<2a,所以x>2a时,f(x)为增函数,x<0时,f(x)为增函数;
由f'(x)<0得,0<x<2a,考虑定义域,当0<x<a,f(x)为减函数,a<x<2a时,f(x)为减函数;
③当a<0时,
由f'(x)>0得,x>0或x<2a,由于此时2a<a<0,所以当x<2a时,f(x)为增函数,x>0时,f(x)为增函数.
由f'(x)<0得,2a<x<0,考虑定义域,当2a<x<a,f(x)为减函数,a<x<0时,f(x)为减函数.
综上,当a=0时,函数f(x)的单调增区间为(-∞,0),(0,+∞).
当a>0时,函数f(x)的单调增区间为x∈(-∞,0),(2a,+∞),单调减区间为(0,a),(a,2a).
当a<0时,函数f(x)的单调增区间为x∈(-∞,2a),(0,+∞),单调减区间为(2a,a),(a,0).
(Ⅱ)①当a≤0时,由(Ⅰ) 可得,f(x)在(1,2)单调增,且x∈(1,2)时,x≠a.
②当0<2a≤1时,即0<a≤
| 1 |
| 2 |
③当1<2a<2时,即
| 1 |
| 2 |
④当2a≥2,即a≥1时,由(Ⅰ)可得,f(x)在(0,a),(a,2a)为减函数,
同时需注意a∉(1,2),满足这样的条件时f(x)在(1,2)单调减,所以此时a=1或a≥2.
综上所述,a≤
| 1 |
| 2 |
点评:本题易忽略函数的定义域,在讨论函数的性质的题目中一定要先求出函数的定义域,在定义域内讨论;难点是分类讨论较复杂,要做到不重不漏,按照数轴从左向右讨论,还要注意特殊情况.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设集合U=R,集合A={x|x2-2x>0},则∁UA等于( )
| A、{x|x<0或x>2} |
| B、{x|x≤0或x≥2} |
| C、{x|0<x<2} |
| D、{x|0≤x≤2} |
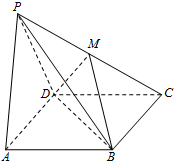 如图,四棱锥P-ABCD中,底面ABCD为矩形,平面PAD⊥平面ABCD.
如图,四棱锥P-ABCD中,底面ABCD为矩形,平面PAD⊥平面ABCD.