题目内容
18.若直线2x-y+a=0与曲线x2+y2-2x=0没有公共点,则实数a的取值范围是a<-2-$\sqrt{5}$或a>-2+$\sqrt{5}$.分析 根据直线与圆没有公共点得到直线与圆的位置关系是相离,则根据圆心到直线的距离大于半径列出关于a的不等式,解不等式即可得到a的范围.
解答 解:把圆x2+y2-2x=0化为标准方程为(x-1)2+y2=1,所以圆心(1,0),半径r=1,
由直线与圆没有公共点得到:圆心(1,0)到直线2x-y+a=0距离d=$\frac{|2+a|}{\sqrt{4+1}}$>r=1,
∴|a+2|>$\sqrt{5}$
∴a<-2-$\sqrt{5}$或a>-2+$\sqrt{5}$
故答案为:a<-2-$\sqrt{5}$或a>-2+$\sqrt{5}$.
点评 此题考查学生掌握直线与圆相离时所满足的条件,灵活运用点到直线的距离公式化简求值,会把绝对值不等式转化为一般的二次不等式进行求解

练习册系列答案
相关题目
8.函数f(x)=cosωxcosθ+sinωxsinθ(ω≠0),对任意x都有f(x)=f($\frac{2π}{3}$-x),则f($\frac{π}{3}$)=( )
| A. | 1或0 | B. | -1或1 | C. | 0 | D. | -1或0 |
10.函数f(x)=lnx+2x-7的零点所在的区间为( )
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
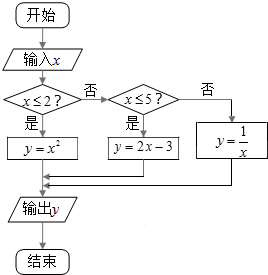 如图,给出了一个程序框图,其作用是输入x的值,输出相应的y的值.
如图,给出了一个程序框图,其作用是输入x的值,输出相应的y的值.