题目内容
2．
如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”．执行该程序框图，若输入a，b的值分别为84，48，则输出的a的值为（ ）| A． | 8 | B． | 12 | C． | 24 | D． | 36 |
分析 由循环结构的特点，先判断，再执行，分别计算出当前的a，b的值，即可得到结论．
解答 解：由a=84，b=48，满足a＞b，
则a变为84-48=36，
由b＞a，则b变为48-36=12，
由a＞b，则，a=36-12=24，
由a＞b，则，a=24-12=12，
由a=b=12，
则输出的a=12．
故选：B．
点评 本题考查算法和程序框图，主要考查循环结构的理解和运用，以及赋值语句的运用，属于基础题．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
12．点P（x，y）是直线kx+y+3=0上一动点，PA，PB是圆C：x2+y2-4y=0的两条切线，A，B是切点，若四边形PACB面积的最小值为2，则k的值为（ ）
| A． | $2\sqrt{2}$ | B． | $±2\sqrt{2}$ | C． | 2 | D． | ±2 |
17．
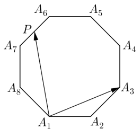如图所示，正八边形A1A2A3A4A5A6A7A8的边长为2，若P为该正八边形边上的动点，则$\overrightarrow{{A_1}{A_3}}•\overrightarrow{{A_1}P}$的取值范围为（ ）
如图所示，正八边形A1A2A3A4A5A6A7A8的边长为2，若P为该正八边形边上的动点，则$\overrightarrow{{A_1}{A_3}}•\overrightarrow{{A_1}P}$的取值范围为（ ）| A． | $[0，8+6\sqrt{2}]$ | B． | $[-2\sqrt{2}，8+6\sqrt{2}]$ | C． | $[-8-6\sqrt{2}，2\sqrt{2}]$ | D． | $[-8-6\sqrt{2}，8+6\sqrt{2}]$ |
7．已知${（{\frac{1}{a}+ax}）^4}+{（{\frac{1}{b}+bx}）^4}$的展开式中x与x3的项的系数之比为1：4，则a4+b4的最小值为（ ）
| A． | 16 | B． | 12 | C． | 8 | D． | 4 |
14．某综艺节目为增强娱乐性，要求现场嘉宾与其场外好友连线互动．凡是拒绝表演节目的好友均无连线好友的机会；凡是选择表演节目的好友均需连线未参加过此活动的3个好友参与此活动，以此下去．
（Ⅰ）假设每个人选择表演与否是等可能的，且互不影响，则某人选择表演后，其连线的3个好友中不少于2个好友选择表演节目的概率是多少？
（Ⅱ）为调查“选择表演者”与其性别是否有关，采取随机抽样得到如表：
①根据表中数据，是否有99%的把握认为“表演节目”与好友的性别有关？
②将此样本的频率视为总体的概率，随机调查3名男性好友，设X为3个人中选择表演的人数，求X的分布列和期望．
附：K2=$\frac{{n{{（{ad-bc}）}^2}}}{{（{a+b}）（{c+d}）（{a+c}）（{b+d}）}}$；
（Ⅰ）假设每个人选择表演与否是等可能的，且互不影响，则某人选择表演后，其连线的3个好友中不少于2个好友选择表演节目的概率是多少？
（Ⅱ）为调查“选择表演者”与其性别是否有关，采取随机抽样得到如表：
| 选择表演 | 拒绝表演 | 合计 | |
| 男 | 50 | 10 | 60 |
| 女 | 10 | 10 | 20 |
| 合计 | 60 | 20 | 80 |
②将此样本的频率视为总体的概率，随机调查3名男性好友，设X为3个人中选择表演的人数，求X的分布列和期望．
附：K2=$\frac{{n{{（{ad-bc}）}^2}}}{{（{a+b}）（{c+d}）（{a+c}）（{b+d}）}}$；
| P（K2≥k0） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
11．在△ABC中，$B=\frac{π}{6}$，BC边上的高等于$\frac{{\sqrt{3}}}{9}BC$，则cosA=（ ）
| A． | $\frac{{5\sqrt{13}}}{26}$ | B． | $-\frac{{5\sqrt{13}}}{26}$ | C． | $-\frac{{3\sqrt{39}}}{26}$ | D． | $\frac{{3\sqrt{39}}}{26}$ |