题目内容
12.点P(x,y)是直线kx+y+3=0上一动点,PA,PB是圆C:x2+y2-4y=0的两条切线,A,B是切点,若四边形PACB面积的最小值为2,则k的值为( )| A. | $2\sqrt{2}$ | B. | $±2\sqrt{2}$ | C. | 2 | D. | ±2 |
分析 由“若四边形面积最小,则圆心与点P的距离最小时,即距离为圆心到直线的距离时,切线长PA,PB最小”,最后利用点到直线的距离求出直线的斜率即可.
解答 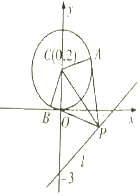 解:如图,${S_{PACB}}=2{S_{△PAC}}=|{PA}|•|{AC}|=2|{PA}|=2\sqrt{{{|{PC}|}^2}-{{|{AC}|}^2}}=2\sqrt{{{|{PC}|}^2}-4}$,
解:如图,${S_{PACB}}=2{S_{△PAC}}=|{PA}|•|{AC}|=2|{PA}|=2\sqrt{{{|{PC}|}^2}-{{|{AC}|}^2}}=2\sqrt{{{|{PC}|}^2}-4}$,
∴当|PC|最小时,面积取最小值,而|PC|最小即为点C到直线l的距离d,
又$d=\frac{5}{{\sqrt{{k^2}+1}}}$,
∴$2\sqrt{{d^2}-4}=2⇒{k^2}=4⇒k=±2$.
故选D.
点评 本题的考点是直线与圆的位置关系,主要涉及了构造四边形及其面积的求法,解题的关键是“若四边形面积最小,则圆心与点P的距离最小时,即距离为圆心到直线的距离时,切线长PA,PB最小”属于中档题.

练习册系列答案
相关题目
2.定义在R上的函数f(x)的图象关于点(-$\frac{3}{4}$,0)成中心对称,且对任意的实数x都有$f(x)=-f(x+\frac{3}{2})$,f(-1)=1,f(0)=-2,则f(1)+f(2)+…+f(2 017)=( )
| A. | 0 | B. | -2 | C. | 1 | D. | -4 |
3.设函数f(x)在R上存在导函数f'(x),对任意的实数x都有f(x)=4x2-f(-x),当x∈(-∞,0)时,f'(x)+$\frac{1}{2}$<4x.若f(m+1)≤f(-m)+3m+$\frac{3}{2}$,则实数m的取值范围是( )
| A. | $[{-\frac{1}{2},+∞})$ | B. | $[{-\frac{3}{2},+∞})$ | C. | [-1,+∞) | D. | [-2,+∞) |
20.在空间中,下列命题正确的是( )
| A. | 经过三个点有且只有一个平面 | |
| B. | 经过一个点和一条直线有且只有一个平面 | |
| C. | 经过一条直线和直线外一点的平面有且只有一个 | |
| D. | 经过一个点且与一条直线平行的平面有且只有一个 |
7.已知函数$f(x)=lg\frac{1+ax}{1-2x}$是定义在(-b,b)上的奇函数,(a,b∈R且a≠-2),则ab的取值范围是( )
| A. | $({1,\sqrt{2}}]$ | B. | $({0,\sqrt{2}}]$ | C. | $({1,\sqrt{2}})$ | D. | $({0,\sqrt{2}})$ |
17.若函数f(x)在其定义域的一个子集[a,b]上存在实数m(a<m<b),使f(x)在m处的导数f'(m)满足f(b)-f(a)=f'(m)(b-a),则称m是函数f(x)在[a,b]上的一个“中值点”,函数$f(x)=\frac{1}{3}{x^3}-{x^2}$在[0,b]上恰有两个“中值点”,则实数b的取值范围是( )
| A. | $(\frac{2}{3},3)$ | B. | (3,+∞) | C. | $(\frac{3}{2},3)$ | D. | $({\frac{3}{2},3}]$ |
4.在平行四边形ABCD中,对角线AC和BD的交点为M,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,则下列向量中与-$\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$相等的向量是( )
| A. | $\overrightarrow{MA}$ | B. | $\overrightarrow{MB}$ | C. | $\overrightarrow{MC}$ | D. | $\overrightarrow{MD}$ |
 如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入a,b的值分别为84,48,则输出的a的值为( )
如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入a,b的值分别为84,48,则输出的a的值为( )