题目内容
11.求下列函数的导数.(1)$y=({\sqrt{x}+1})({\frac{1}{{\sqrt{x}}}-1})$
(2)$y=\frac{x^2}{{{{({2x+1})}^3}}}+{log_2}x$.
分析 (1)先化简再求导即可,
(2)根据导数的运算法则求导即可.
解答 解:(1)y=($\sqrt{x}$+1)($\frac{1}{\sqrt{x}}$-1)=$\frac{1-x}{\sqrt{x}}$=$\frac{1}{\sqrt{x}}$-$\sqrt{x}$=${x}^{-\frac{1}{2}}$-${x}^{\frac{1}{2}}$,
∴y′=-$\frac{1}{2}$${x}^{-\frac{3}{2}}$-$\frac{1}{2}$x${\;}^{-\frac{1}{2}}$,
(2)y′=$\frac{2x(2x+1)^{3}-{x}^{2}((2x+1)^{3})′}{(2x+1)^{6}}$+$\frac{1}{xln2}$=$\frac{2x(2x+1)^{3}-6{x}^{2}(2x+1)^{2}}{(2x+1)^{6}}$+$\frac{1}{xln2}$=$\frac{2x-2{x}^{2}}{(2x+1)^{4}}$+$\frac{1}{xln2}$
点评 本题考查导数的计算,关键是掌握导数的计算公式.

练习册系列答案
相关题目
6.已知函数$f(x)=\left\{\begin{array}{l}{log_2}({{x^2}+x+a}),x≥1\\ 1-{x^2},x<1\end{array}\right.$的值域为R,则常数a的取值范围是( )
| A. | [0,+∞) | B. | (-2,-1] | C. | (-2,0] | D. | (-∞,0] |
16.执行如图所示的程序框图,则输出的b值等于( )
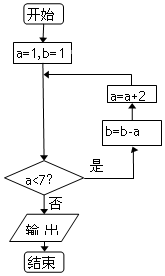

| A. | -24 | B. | -15 | C. | -8 | D. | -3 |
20.下列语句中,不能成为命题的是( )
| A. | 6>10 | B. | x>2 | C. | 若$\overrightarrow{a}$⊥$\overrightarrow{b}$,则$\overrightarrow{a}$•$\overrightarrow{b}$=0 | D. | 0∈N |