题目内容
数列{an}的前n项和为Sn,a1=1,an+1=2Sn+1(n∈N*),等差数列{bn}满足b3=3,b5=9.
(1)分别求数列{an},{bn}的通项公式;
(2)设cn= (n∈N*),求证:cn+1<cn≤
(n∈N*),求证:cn+1<cn≤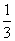 .
.
解:(1)由an+1=2Sn+1①,
得an=2Sn-1+1(n≥2,n∈N*)②,
①-②得an+1-an=2(Sn-Sn-1),
∴an+1=3an(n≥2,n∈N*),
又a2=2S1+1=3,∴a2=3a1,∴an=3n-1.
∵b5-b3=2d=6,∴d=3,∴bn=3n-6.
(2)证明:∵an+2=3n+1,bn+2=3n,
 ∴cn+1<cn<…<c1=
∴cn+1<cn<…<c1=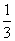 ,
,
即cn+1<cn≤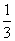 .
.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
 =________.
=________. =
= ,则
,则 的值为________.
的值为________.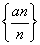 是递增数列;
是递增数列; 过一、三象限的渐近线平行且距离为
过一、三象限的渐近线平行且距离为 的直线方程为 .
的直线方程为 .  的左、右焦点分别为
的左、右焦点分别为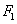 、
、 ,
, 为原点.
为原点.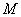 为椭圆
为椭圆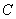 上的一点,
上的一点, 是
是 的中点,且
的中点,且 ,求点
,求点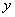 轴的距离;
轴的距离; 与椭圆
与椭圆 、
、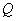 两点,若在椭圆
两点,若在椭圆 ,使四边形
,使四边形 为平行四边形,求
为平行四边形,求 的取值范围.
的取值范围.

 ,
, ,
, ,则
,则 B.
B.  C.
C.  D.
D. 
 ,那么2α-
,那么2α- 的取值范围是( )
的取值范围是( )